Polynome
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 17:47
par Sapeur » 28 Déc 2009, 17:47
Voici le dernier

On donne le polynôme P(x)=(2x-3)(4x²+4x+1)
A. Calculer P(-

)
B. Factoriser 4x²+4x+1
C. Pour quelles valeurs de x a-t-on P(x)=0
D. Resoudre l'équation d'inconnue réelle x :
(2x-3)(4x²+4x+1)=0
Donc pour le A. J'ai trouver
P(-

)=(2X-

-3)(4 X -

²+4 X -

+1)
P(-

)=(-1-3)(1+2+1)
P(-

)= -4 X 4
P(-

)= -16
Pour Le B. Je pense qui faut utiliser la Formule
a(x-x')(x-x'') mais je n'arrive pas a l'apliquer.
Le reste je ne sais vraiment pas du tout.
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 28 Déc 2009, 17:49
par Billball » 28 Déc 2009, 17:49
pour la B tu reconnais pas une identité remarquable?
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 17:52
par Sapeur » 28 Déc 2009, 17:52
(2x²+1)² :we:
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 18:15
par Sapeur » 28 Déc 2009, 18:15
Une idée pour le C & D ??
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 18:18
par Sapeur » 28 Déc 2009, 18:18
Je pense que pour C il faut utiliser la formule Delta b²-4ac
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 18:36
par flo22 » 28 Déc 2009, 18:36
Tu as une petite erreur dans ta factorisation, revérifie. Pour le C, tu dois bien sûr te servir de ta factorisation, te ramenant ainsi à une équation produit de degré 1.
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 19:00
par Sapeur » 28 Déc 2009, 19:00
Effectivement.
Je dirais (2x+1)²
Merci. =)
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 19:10
par Sapeur » 28 Déc 2009, 19:10
Pour le C.
Je trouve Ceci.
4x²+4x+1=0
Soit a=4 b=4 c=1
;)=b²-4ac Soit
;)=(4²)-4 x 4 x 1
;)=-32
Donc pas de solution.
Es-ce Juste ??
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 19:15
par flo22 » 28 Déc 2009, 19:15
Tu as fait une erreur de calcul.
Mais réfléchis bien : tu as factorisé ton expression, tu as donc une autre forme qui permet de donner immédiatement les racines, pas besoin de sortir l'artillerie lourde !
Tu l'as trouvé toi même, on a 4x²+4x+1=(2x+1)² , n'en déduis-tu pas tout de suite les racines ?
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 19:40
par Sapeur » 28 Déc 2009, 19:40
flo22 a écrit:Tu l'as trouvé toi même, on a 4x²+4x+1=(2x+1)² , n'en déduis-tu pas tout de suite les racines ?
Euh Non... La je vois pas :triste:
Pour l'erreur de calcul effectivement. Le resultat est 0 donc 1 solution
x'=

x'=

x'=

x'=
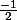
Soit x'=-0.5
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 19:52
par flo22 » 28 Déc 2009, 19:52
Exact.
Mais tu as 4x²+4x+1=(2x+1)². Pourquoi calculer un déterminant ???
Résoudre 4x²+4x+1=0, c'est la même chose que résoudre (2x+1)²=0 !
Et ne peux-tu pas résoudre (2x+1)²=0 sans calculer de discriminant ?
C'était d'ailleurs le but de la question B, factoriser pour ensuite résoudre plus facilement : quelqu'un qui ne sait pas résoudre équation du second degré avec delta aurait quand-même pu résoudre ton exercice, grâce justement à cette factorisation !
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 19:54
par Sapeur » 28 Déc 2009, 19:54
Ok OK Je vois ce que tu veut dire. :we: C'est vrai que c'est plus facile. Merci ;)
Pour le D Tu pourrais m'aider ??
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 20:00
par flo22 » 28 Déc 2009, 20:00
N'oublie pas les questions sont liées, et quand on te demande de factoriser, c'est pas que pour faire joli !
As-tu vraiment réfléchi à la D ? Regarde bien. Que vaut P(x) ? Qu'as tu déjà trouvé ?
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 20:11
par Sapeur » 28 Déc 2009, 20:11
P(x) = 0.5
Donc dans l'équation (2x-3)(4x²+4x+1)=0 je remplace tout les x par 0.5 ??
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 20:17
par flo22 » 28 Déc 2009, 20:17
Non. On te demande de résoudre, c'est à dire trouver toutes les valeurs de x telles que (2x-3)(4x²+4x+1)=0. Tu as écris P(x)=0.5 : c'est faux, P(x) dépend de x et vaut P(x)=(2x-3)(4x²+4x+1) !
Là, il faut résoudre une équation produit : pour (2x-3)(4x²+4x+1)=0, il faut quoi ?
D'une part, que ....=0 ou bien que ....=0.
Je te laisse compléter les petits points.
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 20:25
par Sapeur » 28 Déc 2009, 20:25
J'ai compris ( Enfin je pense...)
2 x - 3 = 0
2 x = 3
x =
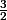
et
2 x + 1 = 0
2 x = -1
x =
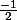
:we:
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 20:49
par flo22 » 28 Déc 2009, 20:49
Oui c'est ça ! Au passage, tu n'avais pas besoin de résoudre 2 x + 1 = 0, tu l'as déjà fait à la question précédente ;)
Juste comme ça, t'es en quelle classe ?
-
Sapeur
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Déc 2009, 13:18
-
 par Sapeur » 28 Déc 2009, 20:51
par Sapeur » 28 Déc 2009, 20:51
1ere Bac Pro Service en Milieu Rural
-
flo22
- Membre Relatif
- Messages: 185
- Enregistré le: 08 Oct 2006, 18:01
-
 par flo22 » 28 Déc 2009, 20:55
par flo22 » 28 Déc 2009, 20:55
Ok ! Ben bon courage pour la suite :)
-
nurarihyon
- Messages: 4
- Enregistré le: 28 Déc 2009, 20:28
-
 par nurarihyon » 28 Déc 2009, 21:02
par nurarihyon » 28 Déc 2009, 21:02
Voici le dernier ;)
On donne le polynôme P(x)=(2x-3)(4x²+4x+1)
A. Calculer P(-)
B. Factoriser 4x²+4x+1
utilises l'indentité remarquable (a+b)au carré
C. Pour quelles valeurs de x a-t-on P(x)=0
il suffit qu'un des deux soit nul alors tu le fais avec 2X-3 ou X=3 demis
D. Resoudre l'équation d'inconnue réelle x :
(2x-3)(4x²+4x+1)=0
Donc pour le A. J'ai trouver
P(- )=(2X--3)(4 X -²+4 X -+1)
P(-)=(-1-3)(1+2+1)
P(-)= -4 X 4
P(-)= -16
Pour Le B. Je pense qui faut utiliser la Formule
a(x-x')(x-x'') mais je n'arrive pas a l'apliquer.
Le reste je ne sais vraiment pas du tout
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
