Dm : calculs de dérivée
45 messages
- Page 2 sur 3 - 1, 2, 3
tu te trompes de formule. elle sert a calculer un terme et non pas la somme des termes.
pour determiner la raison, on sait qu'une suite est geometrique lorsqu'on multiplie toujours par le meme nombre pour passer d'un terme au suivant:
par quel nombre multiplie t on pour passer de 1 a x ou pour passer de x a x² ou de x² a x^3 ?
c'est a dire que la suite et geometrique de raison.... et le premier terme est uo=...
la formule pour la somme des temes d'une suite geometrique est S=uo*((raison^nombre de terme)-1)/(raison-1)
pour determiner la raison, on sait qu'une suite est geometrique lorsqu'on multiplie toujours par le meme nombre pour passer d'un terme au suivant:
par quel nombre multiplie t on pour passer de 1 a x ou pour passer de x a x² ou de x² a x^3 ?
c'est a dire que la suite et geometrique de raison.... et le premier terme est uo=...
la formule pour la somme des temes d'une suite geometrique est S=uo*((raison^nombre de terme)-1)/(raison-1)
c'est ca
mais du coup, on tombe directement sur le pseudo petit b) directement. c'est etrange...
ca m'etonne... il y aurait une methode un peu plus bourine qui consiterait a calculer (x 1 )f(x)= (x 1 )((20 sigma k=0) x^k = 1 + x + x^2 +.. + X^20 )
je me demande si finalement ce n'est pas ce que ton prof attend de toi
mais du coup, on tombe directement sur le pseudo petit b) directement. c'est etrange...
ca m'etonne... il y aurait une methode un peu plus bourine qui consiterait a calculer (x 1 )f(x)= (x 1 )((20 sigma k=0) x^k = 1 + x + x^2 +.. + X^20 )
je me demande si finalement ce n'est pas ce que ton prof attend de toi
en fait elle est tres simple tu as simplement a developper (x 1 )( 1 + x + x^2 +.. + X^20 ) c'est long mais assez simple, tu vas vite voir que pas mal de choses se simplifie
pour la 5) il suffit que tu remarques que l'expression coorespond a f'(x) pour une valeur precise de x. aides toi du 4)a pour comprendre qu'elle valeur de x a été prise et a l'aide du 4)b tu peux en deduire l'expression
bon courage
pour la 5) il suffit que tu remarques que l'expression coorespond a f'(x) pour une valeur precise de x. aides toi du 4)a pour comprendre qu'elle valeur de x a été prise et a l'aide du 4)b tu peux en deduire l'expression
bon courage
lol66 a écrit:enfin si tu préfère qu'on essaie cette solution que tu me propose c'est toi qui voit au moins j'aurais appris une méthode en plus.
apres un petit moment de discussion avec moi meme, il me semble qu'il faut utiliser la methode "bourrine" sinon il y aurait aucun interet a la suite de la question
Je vais tout récapituler pour que vous me disiez si j'ai fais une erreur ou pas :
1) f(1)=21
2) a)(x1)f(x)=(x-1)(20 sigma k=0)x^k=(x-1)(1+x+x^2+...+x^20)=x^21-1
b) somme des termes d'une suite geometrique :
S=(x^21-1)/x-1)
3) f(x) est une fonction polynome donc derivable en R
4)a)f'(x)=(20 sigma k=0)kx^k-1
b)f'(x)=(20x^21-21x^20+1)/(x-1)^2
1) f(1)=21
2) a)(x1)f(x)=(x-1)(20 sigma k=0)x^k=(x-1)(1+x+x^2+...+x^20)=x^21-1
b) somme des termes d'une suite geometrique :
S=(x^21-1)/x-1)
3) f(x) est une fonction polynome donc derivable en R
4)a)f'(x)=(20 sigma k=0)kx^k-1
b)f'(x)=(20x^21-21x^20+1)/(x-1)^2
1) =21) , :++:.
, :++:.
2)a)f(x)=(x-1)\left(\Bigsum_{k=0}^{20}x^k\right)=(x-1)(1+x+x^2+...+x^{20})=x^{21}-1) :++:.
:++:.
b)PAr contre là, si tu veux raisonner en terme de suite, alors il faut le faire bien. Si tu fais la somme des termes d'une suite géometrique alors tu as, pour tout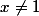 :
:
}{ - (1-x)}=\frac{x^{21} - 1}{x - 1}) .
.
Sinon, si tu raisonne par équivalence, tu fait le produit en croix def(x)=x^{21}-1) .
.
3) f(x) est une fonction polynome donc derivable sur . Une fonction est dérivable sur un ensemble/intervalle.
. Une fonction est dérivable sur un ensemble/intervalle.
4)a)=\Bigsum_{k=0}^{20}kx^k-1) :++: bien ^^.
:++: bien ^^.
b)=\frac{20x^21-21x^20+1}{(x-1)^2}) , ça l'air bon :++:
, ça l'air bon :++:
Et la 5 ?
2)a)
b)PAr contre là, si tu veux raisonner en terme de suite, alors il faut le faire bien. Si tu fais la somme des termes d'une suite géometrique alors tu as, pour tout
Sinon, si tu raisonne par équivalence, tu fait le produit en croix de
3) f(x) est une fonction polynome donc derivable sur
4)a)
b)
Et la 5 ?
45 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
