Petite probleme sur limite

par **newton** » 26 Déc 2009, 19:30

j ai du mal avec les sinus dans les limites
par ex j ai fait
lim x->oo (2x+sinx)/x
posons
u(x)=2x-1/x
v(x)=2x+1/x
pr tt 2x-1<=sinx<=2x+1
pr tt x ux<=fx<=vx or lim x->oo ux=lim x->oo vx=2x+1/x
lim x->oo fx=forme indetermine

voila c pas top je sais

par **Skullkid** » 26 Déc 2009, 19:36

Bonjour, malheureusement tout ne se règle pas en essayant de calquer une méthode vue précédemment sans réfléchir.

Reprenons calmement : pour x tendant vers l'infini on peut écrire

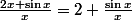
. Peux-tu calculer la limite de

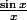
quand x tend vers l'infini ?

par **kamal-maths** » 26 Déc 2009, 20:20

il ya une autre methode et elle est efficace .on l'utlise quand x tend vers +00 ou -00.par exemple lim x->+00(2x+sinx)/2
on sait qye qelque soit x partien à R -1<=>-1+2x<2x+sinx<1+2x
<=>(-1+2x)/xon sais que lim x->+00 -1+2x/x=2
lim x->+00 1+2x/x=2
donc limx_> f(x)=2

par **newton** » 26 Déc 2009, 23:40

bon j etais pas loin dans la methode mais comme je l ai dit j ai pas de cours avec les sinus cosinus tan pour les limites car pour moi une valeur infini pr un sinus c impossible donc je bloque

donc
je ai pensé faire
-1<=>-1+2x<2x+sinx<1+2x
<=>(-1+2x)/xlimx->oo fx=oo

par **zaze_le_gaz** » 26 Déc 2009, 23:46

(-1+2x)/x
par contre (-1+2x)/x et (1+2x)/x ne tendent pas verx l'infini quand x tend vers l'infini

par **newton** » 27 Déc 2009, 00:14

oui oups comme au debut pr moi c une forme indeterminé

par **zaze_le_gaz** » 27 Déc 2009, 00:24

tu peux lever l'indetermination en factorisant le numerateur par x puis en simplifiant par x

par **newton** » 27 Déc 2009, 00:40

x(2+sin)/x
=2+sin
limx->oo fx=2

par **zaze_le_gaz** » 27 Déc 2009, 00:44

quelle horreur!!!!!!!!!! si tu factorise sinx par x alors tu obtiens x((sinx)/x)

le x de sinx est dans le sinus, on ne peut pas l'en sortir comme ca!

il faut lever l'indetermination sur (-1+2x)/x et (1+2x)/x et non pas sur (2x+sinx)/x

ps: le plus beau est que tu trouve une limite correct avec quelque chose de tres faux

par **newton** » 27 Déc 2009, 01:18

:briques: bon je me cache
(2x-1)/x=
x(2-1/x)/x=
2-1/x=2-
(2x+1)/x=
x(2+1/X)/x=
2+1/x=2+
lim fx=2

je suis triste d oublier mon sinus que je controle pas mais tant pis

par **newton** » 27 Déc 2009, 13:33

pouvez me dire si c est bon audessus
car j ai un autre probleme avec
limx->oo sqrt(x+1)-sqrt(x-1)=oo-oo et la je vois pas comment lever l indetermination j arrive pas a factoriser
si enfin j ai fait
sqrt(x(1+1/x)-sqrt(x(1-1/x)
=sqrt(x)sqrt(1+1/x)-sqrt(x)sqrt(1-1/x)

merci de m aider je suis un peu perdu

par **newton** » 27 Déc 2009, 17:38

je suis un peu perdu je suis pas sure du tout de ma premiere limite et encore moins comment faire pour la deuxieme

merci

par **benekire2** » 28 Déc 2009, 10:56

quelqu'un t'as donné la réponse par les gendarmes au dessus, ne te casse pas la tête ...

par **newton** » 28 Déc 2009, 12:05

benekire2 a écrit:quelqu'un t'as donné la réponse par les gendarmes au dessus, ne te casse pas la tête ...

d accord je sais mais je voulais savoir si ma demonstration sur mon post 10 etait valable aussi

sinon pr
lim x->oo sqrt(x+1) - sqrt(x-1)=oo-oo
finalement j ai fait
(sqrt(x+1) - sqrt(x-1))sqrt(x+1) + sqrt(x-1)/sqrt(x+1) + sqrt(x-1)
=0/oo =0

merci

par **zaze_le_gaz** » 28 Déc 2009, 13:42

lim x->oo sqrt(x+1) - sqrt(x-1)=
lim x->oo (sqrt(x+1) - sqrt(x-1))(sqrt(x+1) + sqrt(x-1))/(sqrt(x+1) + sqrt(x-1))
=2/oo =0

pour ton message 10 c'est bon

par **newton** » 28 Déc 2009, 16:32

soit f fx 2x^3-5x²-x+6/x²-3x+2 df R-(1,2)
1- factoriser P=2x^3-5x²-x+6

voila voiou (x-2)(x+1)(2x-3)

(x-2)(x+1)(2x-3)/(x-1)(x-2)
2-etudier la limite de f en 2
lim x->2 f=0

(x-2)(x+1)(2x-3)/x²-3x+2
3-etudier la limite de f en -oo
lim x->-oo f=-oo/+oo=+-oo et la ????

Petite probleme sur limite

petite probleme sur limite

Qui est en ligne