Equation complexe.

par **Mobster** » 23 Déc 2009, 14:36

Bonjour !
Petit exercice (une partie de l'exercice en fait !) :
résoudre

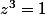
je suppose que mettre que z vaut 1 ne fonctionne pas xD.
Donc j'ai posé z = x + iy, ne sachant pas quoi faire d'autre, et j'ai développé.
Mais je trouve un truc horrible !
Je le marque ou alors je me trompe de méthode ?

par **maturin** » 23 Déc 2009, 14:58

Alors si tu connais la forme exponentielle des complexes c'est super simple à résoudre.

Sinon ton objectif est de trouver les solution de z3-1=0
Tu as trouvé z=1 racine évidente.
Met (z-1) en facteur il te reste un polynome du second degré.

Sais tu trouver les racines complexe d'un polynome du second degré quand le delta est négatif ?

par **Mobster** » 23 Déc 2009, 15:16

Oui, j'ai aussi fait les formes exponentielles, mais j'y ai pas pensé >.< je vais me débrouiller. Merci :)

édit : je vois pas trop en quoi la forme expo peut m'aider..

par **maturin** » 23 Déc 2009, 16:23

si |z^3|=1 que vaut |z| ?
si arg(z^3)=0 quelles valeurs peut valoir arg(z) ?

par **Mobster** » 23 Déc 2009, 16:48

|z| vaut 1, par contre pour l'argument je vois pas pourquoi tu cherches arg(z) en fonction de arg(z^3)=0, car c'est z^3-1=0 non ?

par **Mobster** » 23 Déc 2009, 16:54

Ha non c'est bon j'ai compris --' merci.

par **Mobster** » 23 Déc 2009, 16:58

Donc z^3=1 ssi |z|=1 et ssi arg z = 0 mod 2pi ?

par **zaze_le_gaz** » 23 Déc 2009, 17:09

z^3-1=0

1 est racine evidente donc on peut factoriser notre expression par (z-1)

on otient (z-1)(z²+z+1)=0 reste a resoudre z²+z+1=0

par **maturin** » 23 Déc 2009, 17:16

pose z=m exp(ia)

que vaut z^3
qu'en déduis tu comme équation sur m et sur a

par **Mobster** » 23 Déc 2009, 17:26

Zaze, quand tu dis "on factorise par (z-1)", tu fais quoi exactement ??

par **zaze_le_gaz** » 23 Déc 2009, 17:35

Mobster a écrit:Zaze, quand tu dis "on factorise par (z-1)", tu fais quoi exactement ??

ta question est: comment je trouve la factorisation ou pourquoi je factorise par z-1?

par **Mobster** » 23 Déc 2009, 17:36

Maturin, je vois pas du tout où ça mène... Je crois que je m'y remettrai plus tard, j'ai du mal a suivre la >.<

par **Mobster** » 23 Déc 2009, 17:37

Comment la trouve-tu ?

par **zaze_le_gaz** » 23 Déc 2009, 17:42

je le fais de tete XD

la vrai methode consiste a dire que si on factorise un polynome de degré 3 par (z-1) alors le deuxieme membre de la factorisation doit etre un polynome de degré 2 (pour retomber en developpant sur un polynome de degré 3) c a d:

z^3-1=(z-1)(az²+bz+c) ou a,b,c sont des réel a determiner
pour determiner a, b et c, on developpe (z-1)(az²+bz+c) puis on identifie les cooefficients de meme degré

par **Mobster** » 23 Déc 2009, 17:55

D'accord, merci :)
je trouve S={1;-1/2 - iV3/2 ; -1/2 + iV3/2}. V symbolise les racines carrées. C'est correct ?

par **maturin** » 24 Déc 2009, 10:07

pour la méthode avec exponentielle.

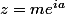
avec m le module réel positif et a l'argument réel.
d'où

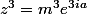
ce qui est la forme exponentielle de z (car m^3 réel positif et a réel)

Tu sais que

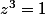
Donc pour

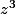
tu as: module = 1 et argument = 0 [2pi]

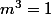
avec m réel => m=1
3a=0 [2pi] => a=2kpi/3
soit a=0 ou a=2pi/3 ou a=-2pi/3 si tu veux exprimer l'argument sur ]-pi,pi]

Tes solutions sont donc

Tu retrouves bien ta solution si tu écris la forme m(cos(a)+isin(a))

Rq: le nombre complexe

est un grand classique souvent noté j.

par **Mobster** » 24 Déc 2009, 14:11

Ha bah justement pour la suite de l'exercice on note j la solution de partie imaginaire positive. Merci beaucoup ! Selon toi c'est "plus mathématique" avec les formes exponentielles ou avec le calcul plus simple des deux facteurs egaux à 0 ?

par **maturin** » 24 Déc 2009, 14:48

Les deux sont mathématiques.
La solution avec exponentielles est plus géométrique, car très facilement visible sur un dessin, et est donc plus immédiate. Quand tu seras habitué à te servir de dessin pour les complexes, tu pourras meme donner la solution sous forme exponentielle sans réfléchir.

La solution résolution d'équation est anaylitique.

Au niveau de la rédaction la seconde est plus simple car tu n'as pas à gérer les modulo 2pi.
Après perso je préfère la géométrique où tu peux suivre ce que tu fais sur un dessin et donc moins de risque d'erreur de calcul.

Equation complexe.

Equation complexe.

Qui est en ligne