Intégrale pour calculer distance moyenne cercle/axe

[bw.segault]

Bonjour,

Je travaille dans la robinetterie, j'ai un problème à résoudre et je sèche lors de la résolution:

LE PROBLEME MATHEMATIQUE:
-------------------------
je n'arrive pas à calculer la distance moyenne entre un axe et un cercle dont le plan est distant de X par rapport à l'axe…

LE CONTEXTE CONCRET:
--------------------
calculer le couple de maoeuvre d'une vanne à boisseau sphérique, couple engendré en bonne partie par les frottements de la boule sur ses sièges.
Pour info une vanne à boisseau sphérique c'est une vanne dont l'opercule est constitué par une boule percée, sur laquelle viennent s'appuyer de façon étanche 2 sièges qui "prolongent" les 2 orifices de la vanne (entrée/sortie) donc un de chaque coté. Et selon comment se positionne la boule par une manoeuvre de rotation, tantôt le trou laisse passer le fluide, tantôt le trou n'est plus en regard avec les orifices et ne voit plus de fluide passer au travers.

J'ai tenté un truc en coordonnées sphériques mais j'arrive à une expression que je ne sais pas intégrer… j'avais déjà eu le problème pour calculer l'intersection d'une droite avec un cercle… Lacunes…

d'avance merci!!

[Ben314]

A ta place, je dirait que le cercle, c'est l'ensemble des points de coordonnées (R.cos(t),R.sin(t),0) (dans le plan z=0) et que l'axe a pour équation par exemple x quelconque, y=0 et z=D (ou D est la distance du plan à l'axe).
Sait tu calculer la distance d'un point quelconque (x,y,z) à un tel axe ? (c'est assez facile)
Puis tu fait le calcul avec le point (R.cos(t),R.sin(t),0), tu intégre le résultat de 0 à 2pi puis tu divise par 2pi (c'est la notion de "moyenne" pour des variables 'continues')...

P.S. : Je n'ais pas fait les calculs...

P.S.2 (5mn plus tard) : j'ai fait les calculs et... il me semble que l'on ne sait pas exprimer la valeur de l'intégrale avec les fonctions usuelles (ln, exp, sin, arctan,...) il faut utiliser les "fonctions éliptiques" pour exprimer la solution.
Bien sûr, pour D et R connus, on peut donner des approximations aussi précise que l'on veut de la valeur en utilisant un ordinateur ou une calcul. qui sait approximer des intégrales...

[bw.segault]

snif je m'attendais à pouvoir en tirer une expression en fonction de R et D... j'ai fait les calculs tels que suggérés et je retombe sur mon intégrale de la forme racine(A+B.sin(teta)²) que je ne sais pas intégrer!
le but était d'avoir ça dans un fichier excel pour refaire les calculs en essayant différentes valeurs de R et D...
merci quand même

[Ben314]

Tu peut avec Excell, en t'y prenant bien "modéliser" un calcul d'intégrale avec la méthode des rectangles (ou des trapèze, ou d'autres méthodes... : regarde sur wikipédia) et donc obtenir la valeur numérique de ton intégrale :
Par exemple la "méthode des rectangles" (la plus simple mais... la moins précise) :
avec N "assez grand"

[bw.segault]

on ne peut pas faire ce genre de somme sur excel à ma connaissance non?

[Ben314]

Une façon de le faire sous Excel est d'utiliser deux "grandes" lignes de longueur N :
Dans la première tu met 0 puis dans chaque case la formule pour avoir 1 de plus que la case précédente (tu fait évidement un "coller" la formule dans toute la ligne) : cette ligne représente 'k'
Dans la seconde ligne tu met dans toutes les cases la formule de (en faisant un 'coller' dans toute la ligne)
Tu n'as plus qu'a prévoir une case qui calcule fois la somme de la deuxième ligne.
Le problème, c'est qu'avec la méthode des rectangles, je pense qu'il faut que N soit assez grand (de l'ordre de la centaine ??) pour avoir un peu de précision.
Donc il peut sembler judicieux de prendre une méthode un peu plus 'rapide' (autre méthode de calcul de l'intégrale ou développement en série entière ou de Fourrier ou ... de la 'fonction éliptique' dont tu as besoin...)

Si j'ai un peu de temps, je regarderais quelles sont les méthodes rapides pour approximer la fonction éliptique dont tu as besoin... (mais tu peut essayer avec la méthode des rectangles...)

[bw.segault]

Ce que je voulais dire c'est qu'il n'y avait pas de fonction "somme sur n termes" utilisable pour une fonction quelconque sur excel.
J'ai donc fait la même chose que ce que tu me suggères mais en colonnes au lieu des lignes (plus limitées en nombre maxi). A partir de N=50 j'ai le même résultat qu'avec 5000 (en ne regardant que les 2 premières décimales du résultat).
Il me semble qu'on aurait optimisé N d'un facteur 4 en intégrant sur PI/2 au lieu de 2PI (double symétrie).

C'est vrai que j'aurai préféré n'avoir qu'une cellule pour calculer ma valeur dans ma feuille mais ne t'embête pas trop pour moi, ton aide m'a été précieuse et je suis content d'avoir pû un peu réviser mes maths.
MERCI!

[Ben314]

Il n'y as vraiment pas de quoi...
Pour les "optimisations possibles", il y en as... des tas, en particulier, d'utiliser les symétries comme tu le sugère. Tu peut aussi utiliser la "méthode des trapèzes" qui est la même sauf que tu calcule aussi la valeur de f(a+k.(b-a)/N) pour k=N puis dans la somme, tu met un coeff 1/2 devant les valeurs correspondant à k=0 et k=N : ça parrait tout con, mais ça améliore pas mal (il me semble que c'est équivalent à multiplier N par 2)...

Si tu veux un calcul "direct dans la case" il faudrait savoir si sous Excell, on peut "appeler" un programme extérieur pour faire un calcul (calculer la fonction éliptique)
Je pense que c'est possible, mais je ne sais pas du tout comment...

P.S. (au cas ou tu n'y aurait pas pensé) une fois tes deux colonnes "compliquées" remplies, tu dit à Excel de les afficher avec une largeur égale à 0 et... on ne les voit plus....

[bw.segault]

merci encore pour tout, pour le programme externe je vais en rester là je n'ai pas envie de compliquer l'usage de cette feuille qui n'est pas destiné qu'à moi. l'optimisation n'est pas non plus primordiale...
bonne continuation!

[Ben314]

Je sais pas si ça t'interesse toujours, mais aprés quelque calculs, je trouve que, si D et la distanc axe/plan et R le rayon du cercle, la distance moyenne est :
avec
et
et il suffit de prendre les 2/3 premiers termes de la somme pour avoir une approximation trés convenable du résultat. (donc ça tient dans UNE case.....)

[bw.segault]

impressionant, en deux termes (k=0;k=1) j'ai déjà ma valeur à deux décimales près! (identique à celle déterminée avec la méthode des rectangles sur un paquets de termes).
Ce résultat a été calculé avec quelle méthode? J'ai bien peur de ne savoir le refaire moi même mais en tous cas pour ma culture je saurai au moins comment ça a été résolu!
merci!

[Ben314]

Pour donner les "grandes lignes" :
On part de .
1) On remplace par et on fait le changement de variable
2) On met le 'terme constant' en facteur dans la racine et on le sort.
3) On calcule le développement en série entière de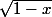 et on l'utilise avec .
4) On permute l'intégrale et la somme (de la série entière) car la série converge uniformément.
5) On calcule les intégrales de la forme soit par récurrence (double) sur n (avec une intégration par parties), soit en écrivant et en développant à l'aide de la formule du binôme de newton.
6) On conclue (les résultent d'un produit des coeff de la série entière de 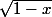avec un coeff binomial...)

P.S. : La formule est extrèmement efficace lorsque n'est pas trop proche de 1, c'est à dire pas trop petit par rapport à . On pourrait sans doute trouver un autre développement plus rapide lorsque est petit devant ...

[bw.segault]

wouaw! Et bien je m'arrêterai là dans mes recherches :-) mais je garde ça de coté quand même... non loin de la fameuse case enfin remplie! (un an qu'elle attendait sa formule!).
Une dernière fois merci pour ton aide!