Matrices orthogonales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 12:38
par HanZel » 20 Déc 2009, 12:38
Bonjour à tous,
Je cherche à montrer que l'ensemble des matrices orthogonales
)
est une sous variété de
)
Je pose
=^tMM-I)
ainsi,
 \; f(M)=0)
Je différentie :
)
et
)
on a :
(H)=^tMH +^tHM)
J'aimerai bien que
)
soit surjective ! :happy2:
Je ne sais pas comment m'y prendre...
 = \{ H \in M_n(\mathbb{R}) \; | \; ^tMH +^tHM=0\})
je n'arrive pas à le résoudre...
Je me pose quelques questions :
Est ce que
 \in \mathcal{L}_c(M_n(\mathbb{R})\, , \, M_n(\mathbb{R})))
? => Endomorphisme? => Si Ker df(M) = 0 alors df(M) surjective?
Je pensais utiliser le théorème du rang mais je ne connais pas la dimension du noyau..
Pouvez vous m'aider un peu.
Merci !

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 12:48
par Ben314 » 20 Déc 2009, 12:48
Salut.
Ta méthode est bonne modulo deux remarques :
1) Il faut non seulement écrire que f(M)=0 pour tout M dans O_n(R), mais évidement écrire que c'est une équivalence.
2) Il faut effectivement montrer que df est surjective, mais surement pas avec M_n(R) comme ensemble d'arrivé car si c'était vrai cela montrerais que O_n(R) est une variété de dimension... 0 !!!
Regarde un peu mieux la fonction f et tu devrait voir que l'on peut prendre un ensemble d'arrivé "plus petit"...
De plus, tu doit étudier l'éventuelle surjectivité de df uniquement en des "points" M de O_n(R)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 12:59
par HanZel » 20 Déc 2009, 12:59
L'ensemble d'arrivé de f est l'ensemble des matrices symétriques Sym(n,R).
Alors
 \in \mathcal{L}_c(O_n(\mathbb{R})\,,\,Sym(n,\mathbb{R})))
?

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 13:11
par Ben314 » 20 Déc 2009, 13:11
Oui, c'est nettement mieux....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 13:20
par Ben314 » 20 Déc 2009, 13:20
Pour
)
, je peux te filler un "petit coup de pouce":
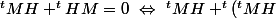=0\ \Leftrightarrow\ ^tMH)
est...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 13:28
par HanZel » 20 Déc 2009, 13:28
dim Sym(n,R)= n(n+1)/2 si j'ai la dimension de Ker(df(M)) je pourrais trouver la dim de Im(df(M)) avec dim Ker(df(M)) + dim Im(df(M)) = dim Sym(n,R).
Et si dim Im(df(M)) = dim Sym(n,R) alors df(M) est surjective si j'ai bien compris ?

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 13:31
par Ben314 » 20 Déc 2009, 13:31
HanZel a écrit:dim Sym(n,R)= n(n+1)/2 si j'ai la dimension de Ker(df(M)) je pourrais trouver la dim de Im(df(M)) avec dim Ker(df(M)) + dim Im(df(M)) = dim Sym(n,R).
Et si dim Im(df(M)) = dim Sym(n,R) alors df(M) est surjective si j'ai bien compris ?
C'est exactement le principe, (sauf que dim(ker)+dim(im) n'est pas égal à dim(espace d'arrivé) mais à...)
As tu trouve ker(df) (et donc sa dimension) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 13:39
par HanZel » 20 Déc 2009, 13:39
Oh oui, dim(im)+dim(ker)=dim(depart) !
Pour Ker(df(M)) je n'ai pas trouvé... :triste:

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 13:47
par Ben314 » 20 Déc 2009, 13:47
\ \Leftrightarrow\ ^tMH +^tHM=0\ \Leftrightarrow\ ^tMH +^t(^tMH)=0)
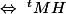
est antisymétrique
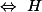
est de la forme...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 14:20
par HanZel » 20 Déc 2009, 14:20
Je ne sais pas si c'est ça mais en tatonant un peu je dirais H est de la forme Identité + Antisymétrique?

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 14:35
par Ben314 » 20 Déc 2009, 14:35
\ \Leftrightarrow\ ^tMH +^tHM=0\ \Leftrightarrow\ ^tMH +^t(^tMH)=0)
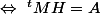
où

est antisymétrique
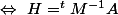
où

est antisymétrique (si M inversible)
L'application
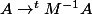
étant linéaire bijective, la dimension de
)
est la même que celle de...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 15:26
par HanZel » 20 Déc 2009, 15:26
J'ai compris mais ça ne me serait pas venu naturellement..
Alors on a : dim
))
= dim Antisym(n,R) grace à la bijectivité de
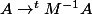
dim
))
= n(n-1)/2
Donc dim Im(n,R)= n²-n(n-1)/2 = n(n+1)/2 = dim Sym(n,R)
Ainsi df(M) est surjective, donc On(R) est une sous variété de Mn(R)
Et la dimension de l'espace tangent en tout en tout point de On(R) est n(n-1)/2

-
Ben314
- Le Ben
- Messages: 21535
- Enregistré le: 11 Nov 2009, 22:53
-
 par Ben314 » 20 Déc 2009, 15:50
par Ben314 » 20 Déc 2009, 15:50
Impeccable.
Pour le coté "ça ne me serait pas venu naturellement", tu peut commencer par évaluer
))
pour M=Id et cela peut donner des idées du cas général.
Une façon plus théorique de voir que le cas M=Id est équivalent au cas général est d'utiliser le fait que O_n(R) est non seulement un espace topologique mais aussi un groupe et de montrer que l'espace tangent en un point M quelconque peut s'obtenir à partir de l'espace tangent en Id...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 02:06
-
 par HanZel » 20 Déc 2009, 16:13
par HanZel » 20 Déc 2009, 16:13
Je vais retenir tes conseils pour les partiels ;)
Merci pour ton aide !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
