PPCM d'un ensemble
15 messages
- Page 1 sur 1
PPCM d'un ensemble
Bonjour,
Lorsque je dois réduire des fractions au meme dénominateur, le PPCM me permet de définir le dénominateur commun.
Mais lorsque j'ai non pas 2 mais 6 fractions, existe-t-il une façon de calculer le PPCM pour 6 nombres ?
Sinon quelle méthode utiilser pour définir un dénominateur commun sur un ensemble de fractions ?
Merci
Lorsque je dois réduire des fractions au meme dénominateur, le PPCM me permet de définir le dénominateur commun.
Mais lorsque j'ai non pas 2 mais 6 fractions, existe-t-il une façon de calculer le PPCM pour 6 nombres ?
Sinon quelle méthode utiilser pour définir un dénominateur commun sur un ensemble de fractions ?
Merci
D'accord, pour additioner 6 fractions avec 6 denominateurs différents:
1/ je décompose l'ensemble des dénominateurs en facteur de nombres premiers
2/ j'identifie le PPCM en prenant le nombre formé de tous les facteurs présents élevés à la puissance max que l'on trouve dans les facteurs
3/ Question subsidiare: quelle est la meilleure méthode pour faire une décomposition en facteurs premiers ?
Par ex, le nombre 270.
Je commence par diviser par 2,3,5,... ou plutot par des grands nombres premiers ?
Merci
1/ je décompose l'ensemble des dénominateurs en facteur de nombres premiers
2/ j'identifie le PPCM en prenant le nombre formé de tous les facteurs présents élevés à la puissance max que l'on trouve dans les facteurs
3/ Question subsidiare: quelle est la meilleure méthode pour faire une décomposition en facteurs premiers ?
Par ex, le nombre 270.
Je commence par diviser par 2,3,5,... ou plutot par des grands nombres premiers ?
Merci
En général, il est bien plus simple de commencer par les petits :
270 se divise par 2 et 270=2x135.
135 ne se divise pas par 2, mais par 3 : 135=3x45
45 se divise encore par 3 : 45=3x15
15 se divise aussi par 3 : 15=3x5 et 5 est premier
donc 270=2x3x3x3x5
Sinon, pour calculer le pgcd de plus de deux nombre, tu peut le faire de proche en proche:
pgcd des 2 premier puis
pgcd de (pgcd des 2 premiers) et du 3em
.
.
.
P.S. il vaut mieux commencer par les petits car, si tu prend un nombre au hazard, il est beaucoup plus probable qu'il se divise par 2 que par 101 !!!!
270 se divise par 2 et 270=2x135.
135 ne se divise pas par 2, mais par 3 : 135=3x45
45 se divise encore par 3 : 45=3x15
15 se divise aussi par 3 : 15=3x5 et 5 est premier
donc 270=2x3x3x3x5
Sinon, pour calculer le pgcd de plus de deux nombre, tu peut le faire de proche en proche:
pgcd des 2 premier puis
pgcd de (pgcd des 2 premiers) et du 3em
.
.
.
P.S. il vaut mieux commencer par les petits car, si tu prend un nombre au hazard, il est beaucoup plus probable qu'il se divise par 2 que par 101 !!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut !
Comme il t'a été dit, prends les 6 dénominateurs, décompose-les en facteurs premiers, ex :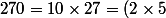\times(9\times3)=2\times3^3\times5) , pas la peine de chercher de gros diviseurs, divise par ce qui semble le plus simple. Puis tu regroupe comme je l'ai fait, tout les mêmes termes entre eux sous forme de puissances. Fais-en de même avec les 5 autres dénominateurs. Une fois cela fait, le ppcm vaut le produit de tous les différents termes de plus hauts degrés, ex :
, pas la peine de chercher de gros diviseurs, divise par ce qui semble le plus simple. Puis tu regroupe comme je l'ai fait, tout les mêmes termes entre eux sous forme de puissances. Fais-en de même avec les 5 autres dénominateurs. Une fois cela fait, le ppcm vaut le produit de tous les différents termes de plus hauts degrés, ex :
On a :



Alors=2^3\times3^3\times5\times7^2 \times{11})
Comme il t'a été dit, prends les 6 dénominateurs, décompose-les en facteurs premiers, ex :
On a :
Alors
Je reprends l'exemple d'avant:
En général, il est bien plus simple de commencer par les petits :
270 se divise par 2 et 270=2x135.
135 ne se divise pas par 2, mais par 3 : 135=3x45
45 se divise encore par 3 : 45=3x15
15 se divise aussi par 3 : 15=3x5 et 5 est premier
donc 270=2x3x3x3x5
Question triviale: comment je sais par quel nombre je peux divisiser ?
Je veux dire, on sent que 270 est divisible par 10, donc par 5, mais est-ce qu'il existe des "règles" quand on travaille avec des nombres très grand ?
Comment je sais qu'un nombre est divisble par deux ? Il est pair ?
Comment je sais qu'un nombre est divisible par trois ?
Comment je sais qu'un nombre est divisible par cinq ?
Merci
En général, il est bien plus simple de commencer par les petits :
270 se divise par 2 et 270=2x135.
135 ne se divise pas par 2, mais par 3 : 135=3x45
45 se divise encore par 3 : 45=3x15
15 se divise aussi par 3 : 15=3x5 et 5 est premier
donc 270=2x3x3x3x5
Question triviale: comment je sais par quel nombre je peux divisiser ?
Je veux dire, on sent que 270 est divisible par 10, donc par 5, mais est-ce qu'il existe des "règles" quand on travaille avec des nombres très grand ?
Comment je sais qu'un nombre est divisble par deux ? Il est pair ?
Comment je sais qu'un nombre est divisible par trois ?
Comment je sais qu'un nombre est divisible par cinq ?
Merci
Il y a des régles évidentes pour la divisibilitè par 2 et 5 ....
Un peu moins évidente pour la divisibilité par 3 (la somme des chiffres doit être divisible par 3)
Encore un peu moins facile pour la divisibilité par 11 (le premier chiffre-le second chiffre+le troisième chiffre-... doit être divisible par 11)
Pour les autres (en particulier 7) les "règles" deviennent trés compliquées : le plus simple est... de sortir la machine...
Un peu moins évidente pour la divisibilité par 3 (la somme des chiffres doit être divisible par 3)
Encore un peu moins facile pour la divisibilité par 11 (le premier chiffre-le second chiffre+le troisième chiffre-... doit être divisible par 11)
Pour les autres (en particulier 7) les "règles" deviennent trés compliquées : le plus simple est... de sortir la machine...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je prépare un examen qui se déroule sans machinele plus simple est... de sortir la machine...
Pour la division par deux: tous les nombres pairs sont divisibles par deux
vrai ?
Pour la division par trois: tous les nombres dont la sommes des chiffres est divisible par trois, vrai ?
Pour la division par cinq: tous les nombres dont le dernier chiffre est soit 0 soit 5 sont divisibles par cinq, vrai ?
Pour 7, il y a une règle pour savoir si un nombre est divisible par 7 ?
UPDATE:
J'ai trouvé les règles pour 7 et 13
7 : nombre de dizaines moins 2 fois les unités doit être divisible par 7
Exemple : 154
15 - 2 * 4 = 7 ; c'est bon car 7 se divise par 7
13 : nombre de dizaines + 4 fois les unités doit être divisible par 13
Exemple : 117
11 + 4 * 7 = 39 ; c'est bon car 39 se divise par 13
UPDATE:
J'ai trouvé les règles pour 7 et 13
7 : nombre de dizaines moins 2 fois les unités doit être divisible par 7
Exemple : 154
15 - 2 * 4 = 7 ; c'est bon car 7 se divise par 7
13 : nombre de dizaines + 4 fois les unités doit être divisible par 13
Exemple : 117
11 + 4 * 7 = 39 ; c'est bon car 39 se divise par 13
Aprés, a moins que tu ne veuille devenir 'calculateur prodige' je sais pas s'il faut apprendre par coeur 36000 formules concernant la divisibilité.
Ca m'étonnerait qu'a un concours on te donne des nombres de 10 chiffre à décomposer en produit de nombres premier...
Ca m'étonnerait qu'a un concours on te donne des nombres de 10 chiffre à décomposer en produit de nombres premier...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 123 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
