Bonjour à tous :)
Voilà j'ai un exercice assez simple à priori, mais je n'arrive pas à prouver mes résultats autre que par le bon sens.
En effet, il faut trouver l'ensemble de points M d'affixe z vérifiant les relations suivantes:
1) module(z+3i) = 6 (cercle de rayon 6 et de centre de coordonnées (-3i))
2) module(zbar + 1 - 2i) = 5 (j'ai pris le conjugué du nombre ce qui fait z + 1 + 2i, c'est donc le cercle de rayon 5 et de centre de coordonnées (-1 -2i) )
3) module(iz - 3) = 1 (là par contre je suis bloqué, si quelqu'un pouvait m'aider :) )
Seulement, ces ensembles ce déduisent de mon bon sens, et j'aimerais savoir comment trouver de façon "algébrique" les coordonnées des centre et les rayons des cercles (mon professeur étant très rigoureux au niveau de la justification...).
Voilà, si quelqu'un pouvait me proposer un moyen de rédiger cet exercice, cela me serait très utile :)!
En vous remerciant d'avance,
Zack
Recherche d'ensemble de point (plan complexe): rédaction
8 messages
- Page 1 sur 1
bonjour,
pour le 3), tu peut utiliser le fait que pour (de nouveau) te ramener à l'équation d'un cercle...
pour (de nouveau) te ramener à l'équation d'un cercle...
Si tu veut faire "rigoureusement" les calculs une méthode (pas la plus rapide, mais la plus évidente) consiste à écrire z=x+iy et à écrire les équations en x et y en utilisant la formule donnant le module en fonction de la partie réelle et imaginaire.
Une méthode plus astucieuse peut consister à partir de la formule (où
(où 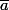 est le conjugué de a)...
est le conjugué de a)...
Une troisième méthode peut consister, en partant d'un des cercle, à dire qu'un point (x,y) appartient au cercle de centre (xo,yo) de rayon r si et seulement si il existe tel que
tel que ) et
et ) ...
...
Il y a surement d'autres méthodes... choisi ta voie....
pour le 3), tu peut utiliser le fait que
Si tu veut faire "rigoureusement" les calculs une méthode (pas la plus rapide, mais la plus évidente) consiste à écrire z=x+iy et à écrire les équations en x et y en utilisant la formule donnant le module en fonction de la partie réelle et imaginaire.
Une méthode plus astucieuse peut consister à partir de la formule
Une troisième méthode peut consister, en partant d'un des cercle, à dire qu'un point (x,y) appartient au cercle de centre (xo,yo) de rayon r si et seulement si il existe
Il y a surement d'autres méthodes... choisi ta voie....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci beaucoup pour le 3) donc ça fait module(z-3) = 1 au final non?
Par contre pour le reste euh, franchement j'ai du mal à voir où tu veux en venir lol. Si tu as le temps pourrais-tu me traiter un exemple, avec module (z+3i)= 6 par exemple s'il te plait? :)
J'ai commencé récemment avec les complexes et je maîtrise pas trop ce concept encore...
Merci bien :)
Par contre pour le reste euh, franchement j'ai du mal à voir où tu veux en venir lol. Si tu as le temps pourrais-tu me traiter un exemple, avec module (z+3i)= 6 par exemple s'il te plait? :)
J'ai commencé récemment avec les complexes et je maîtrise pas trop ce concept encore...
Merci bien :)
zack a écrit:Pour le 3) donc ça fait module(z-3) = 1 au final non?
pas vraiment :
Si tu ne maitrise pas tout, j'aurais tendance à conseiller la méthode 1) qui utilise simplement le fait que
Par exemple, si on écrit
Ensuite, une petite "indic.", si tu as deux équations de ce type, écrit la différences entre les deux...
P.S. une deuxième "indic." : les calculs se terminent par une équation du second degrés, ce qui est normal car l'intersection de deux cercles c'est 0,1 ou 2 points...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je suis en train de voir que mes "indics." sont complètement inutiles (y compris les calculs au dessus).
J'avais survolé l'énoncé est je croyait que tu devait déterminer les complexes qui vérifient plusieurs équations c'est à dire déterminer l'intersection de plusieurs cercles.
Mais ce n'est pas ça du tout !!!!!
On te demande juste de déterminer l'ensemble des point tels que....
Donc la seule chose que tu as besoin d'utiliser c'est que si A et B sont deux points d'affixe a et b alors la distance AB est |b-a|... (surement vu en cours : c'est 'presque' la définition du module)
Désolé...
J'avais survolé l'énoncé est je croyait que tu devait déterminer les complexes qui vérifient plusieurs équations c'est à dire déterminer l'intersection de plusieurs cercles.
Mais ce n'est pas ça du tout !!!!!
On te demande juste de déterminer l'ensemble des point tels que....
Donc la seule chose que tu as besoin d'utiliser c'est que si A et B sont deux points d'affixe a et b alors la distance AB est |b-a|... (surement vu en cours : c'est 'presque' la définition du module)
Désolé...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ah pas de soucis, mais ta méthode peut aussi marcher pour trouver nan? Car je trouve des équations de cercles, donc ça doit être sûrement possible...
Et juste une question: A-t-on le droit de mettre dans le plan complexe qu'une droite a une équation y= -2i? Je veux dire, cette notation est-elle aussi valable dans le plan complexe?
Et juste une question: A-t-on le droit de mettre dans le plan complexe qu'une droite a une équation y= -2i? Je veux dire, cette notation est-elle aussi valable dans le plan complexe?
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
