Injectivité chez les complexes

[Lucanae]

Bonjour!
Je suis actuellement en fac de math-info, première année, et je rencontre un petit soucis.
Je suis en train d'étudier l'injectivité de fonctions dans l'ensemble des complexes, et je bloque sur une fonction bien particulière:
f: C --> C
z --> z^3
Je sais que f injective <=> [ f(z) = f(a) <=> z = a]
<=> [z^3 = a^3 <=> z = a] *
Il faut que je montre la proposition à la dernière ligne (ligne *), mais je ne sais pas comment faire. Pourriez-vous me donner une petite piste svp?

Merci d'avance!

Lucanae

[alavacommejetepousse]

bonjour

et si par hasard tu devais montrer qu elle n est pas injective que ferais tu ?

[Lucanae]

Pour montrer qu'elle n'est pas injective, soit je montre que par mon raisonnement, j'arrive à un truc faux, donc non-injective, ou alors je trouve un contre exemple.
Je vais chercher un contre exemple, mais il me semble bien qu'elle soit injective.

[alavacommejetepousse]

voila cherche un contre exemple ( c est à dire?)

[Lucanae]

Trouver un contre exemple revient à trouver deux complexes différents a et z tel que f(z) = f(a).

[alavacommejetepousse]

voila et je te propose a = 1

[Ben314]

Une fois que tu aura trouvé ton contre exemple (à la main), réfléchi une petite minute à la question suivante :
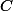
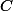
"une fonction polynôme de dans de degrés supérieur où égal à deux peut-elle être injective ?"

[sniperamine]

Bonjour alors tu n'as pas encore trouvé ton contre exemple ? c'est pas difficile !!

[Lucanae]

Merci bien!
J'ai trouvé mon contre exemple, j'ai un peu été ailleurs, car c'était facile.
Ça revient en plus à calculer les racines 3èmes de l'unité!

Un contre exemple: f(1 ) = f(e^((2/3)pi)) = 1.

Pour la suite, du coup, un polynome de C ne peut être injectif!

Merci beaucoup!

Lucanae

[alavacommejetepousse]

bonjour

le du coup est abusif