[Résolue]cos2(z)+sin2(z)=4 z ∈ C

par **Izanagi** » 07 Déc 2009, 18:54

Bonjour,

Voila je cherche à donner un coup de main a quelqu'un qui en a besoin, N'étant pas mathematicien, je me tourne donc vers vous pour soliciter votre aide.

Ainsi toutes âmes serviables et desireuses de faire un beau geste sont les bienvenues. :++:

L'énnoncer est le suivant :

Complex analysis : solve cos2(z)+sin2(z)=4 z ;) C

Un grand merci d'avance

par **Ben314** » 07 Déc 2009, 19:03

Si les 2 de cos2 et sin2 sont des carrés.... ça va être dur....
Comme dans R, cette somme vaut 1 pour tout z de C....

par **Izanagi** » 07 Déc 2009, 19:07

Merci pour cette réponse

Oui les 2 correspondent à des carrés.

J'ai fait quelques recherche et je trouve ce theorem:

sin(

z ) =

sin z , cos(z ) = cos z , sin(z +2k;)) = sin z , cos(z +2k;)) = cos z , sin2 z + cos2 z = 1. :hum:

Ce pourrait-il qu'il y ait une erreur dans l'énnoncer?

par **Epsilon** » 08 Déc 2009, 18:40

par définition:si

est nombre complexe alors

et

comme dans le cas réel
donc pour ton équation :

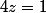
et donc

par **Izanagi** » 08 Déc 2009, 18:51

Un grand merci pour vous être "décarcasser".

Je viens de recevoir une nouvelle notification de mon ami, et il semble bien qu'il y ait une erreur dans l'énnoncer

[Résolue]cos2(z)+sin2(z)=4 z ∈ C

[Résolue]cos2(z)+sin2(z)=4 z ∈ C

Qui est en ligne