Limites de fonctions : critere de Cauchy

[Filam]

Bonjour à tous,

Je rencontre quelques difficultés avec les critères de Cauchy appliqués aux limites de fonctions.

Je vais vous montrer ou je coince par l'intermédiaire d'un exemple :



On cherche la limite :



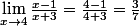
Le premier critère de Cauchy nous dit :

Ssi

On remplace :















C'est maintenant que je coince, dans mon cours il faut majorer ou minorer |x+3| et je ne sais pas ce que je dois faire.
Merci d'avance.

Filam.

[Ben314]

bonjour,
Jusque là, tu as procédé par équivalences. Tu as montré que :


Tu cherche maintenant une implication de la forme :

Réfléchi bien sur le lien qu'il doit y avoir entre et pour qu'une telle implication soit vraie (fait attention, il est trés façile de se tromper).

Peut être, pour encore simplifier, pose toi la question sous la forme :
Quel lien doit-il y avoir entre a et b pour que l'on ait :
?

[Filam]

Ou veux tu en venir ?

[Ben314]

Je veux en venir que tu cherche donc un ? qui soit supérieur à
|(x-4)/(x+3)|
De plus, vu l'objectif de la preuve, il serait agréable que ? soit de la forme
|(x-4)/quelque_chose| et tu n'as plus qu'a te poser la question :
Comment avoir |(x-4)/quelque_chose| >= |(x-4)/(x+3)| ?
et tu aura (enfin) la réponse à ta question : doit-on majorer ou minorer le |x+3|...

[Filam]

Donc ici il faut minorer

3<x
6<x+3

Donc :

|?| =


C'est ca ?

[Ben314]

Impeccable,
En expliquant (comme cela doit être fait dans les exemple donnés par le prof) que, comme on va prendre x proche de 4, ca ne coute pas trés cher de supposer qu'il est strictement plus grand que 3 (ou tout autre type d'explication pour justifier ton 'x>3' du début)

Je pense que tu as parfaitement compris que tu ne pouvais pas écrire 'x>5' à la place mais que tu aurrais pu écrire 'x>0' ou même 'x>-2' (par contre 'x>-3' ne marchais pas...)

[Filam]

Tu peux m'expliquer pourquoi je n'aurais pas pu écrire x>3 ?

Je met x + 3 parceque dans mon cours c'est comme ca, il faut encadre la valeur, hors ici ce n'est pas x mais x+3.

J'aimerais bien avoir ton explication sur la chose. :++:

[Filam]

Enfin il y a pas un erreur la ?

C'est pas |x-3| qu'on a, c'est

:briques:

[Filam]

Je releve la chose parceque dans mon cours on avait écrit ca :

Pour majorer on minore x+3. :marteau:

[Ben314]

Ici, tu ne dois pas perdre de vue que ce que tu cherche à faire, c'est de trouver un (dépendant de ) tel que :
[TEX]| x - 4 | 0, c'est à dire que a3 dans la parenthése de mon avant dernier post est une faute de frappe !!!! il fallait lire x>-3. désolé : je rectifie.

[Filam]

Pourquoi x>5 n'aurait pas fonctionné ?

HAAA ! JE COMPRENDS PLUS RIEN ! :cry: :cry: :cry:

[Filam]

Merci beaucoup en tout cas. Je vais reprendre ca demain a mon aise, ma tete va exploser.

[Ben314]

x>5 "n'aurait pas fonctionné" car tu n'a le droit qu'a des hypothèses de la forme |x-4|5 n'est pas de cette forme.

Pour "parler simplement" (et il faut comprendre que, dans tout le charabia que l'on écrit avec cette "formule de cauchy" il y a des idées trés simple),
Tu veut étudier une fonction f(x) pour x proche de 4.
Tu as donc le droit de supposer que x>3 ou que x3.99
mais surement pas que x>4.1 ou que x<3.7.
Cela devrait parraitre plus simple comme ca....

[Filam]

On cherche la limite :



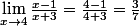
Le premier critère de Cauchy nous dit :

Ssi



Comme

On doit majorer donc on minore x+3
3<x
6<x+3

Ce qui nous donne











That's it ?

[Ben314]

Impeccable à deux "détails" prés :
1) Les lignes avec les ??? et le "a a>=b", à peu prés tout le monde ne les écrit qu'au brouillon (elle te servent seulement à comprendre qu'il faut minorer le x+3. (en particulier les ??? dans une copie "au propre", ca fait un peu con)
2) Il faut par contre donner une petite explication pour justifier ton "3<x" : il apparait... comme un cheveux sur la soupe, c'est à dire que l'on ne voit pas d'où il sort. Personellement, pour le justifier, j'écrirait :
"On peut bien sur supposer que |x-4|<1 c'est à dire que 4-1<x<4+1 et donc ...."

Regarde dans les corrections de ton profs. Il donne forcément quelque part une explication pour justifier que l'on peut supposer que x à certaines propriétées. (l'idée est celle de la fin de mon avant dernier post)

[Filam]

Si je suis venu ici c'est que j'ai du mal à comprendre mon cours et donc les explications données.

Ça n'apparait pas, et mon cours est parfaitement en ordre.

Le prof a même donné des cours de rattrapages ou il a tout ré expliqué mais rien à faire. :doh:

[Filam]

J'ai bien compris la chose, et c'est uniquement grâce a toi ! Merci beacoup !!!


Je vais en faire un autre pour voir si je suis au point pour l'examen. :hum:

[Filam]

On cherche la limite :



Premier critère de Cauchy :

Ssi

doit être majorer donc on minore

On suppose que

[Ben314]

Cette partie là :

doit être majorer donc on minore

Tu la laisse au brouillon, c'est mieux. elle sert juste à comprendre pourquoi tu doit minorer |x-2|

Ensuite, tu ne peut pas prendre x=7 (au niveau intuitif, on fait tendre x vers 7 signifie qu'on le prend tréééééééés proche mais pas égal)
Par contre tu peux écrire (je reprend tes formules) :

On suppose que

Remarques : la partie "a ne mettre qu'au brouillon" fait en fait resurface ici
Donc, pour que il suffit que
Attention à bien comprendre le sens (français) du "il suffit que" qui veut dire que l'implication va de "droite à gauche". C'est normal vu ce que l'on cherche à démontrer.
On termine en écrivant :


Enfin, une "joli conclusion" :
Pour être sûr que , il suffit de prendre x tel que
et
(normalement, il ne faut pas oublier la deuxième inégalité dont on s'est servi dans les calcule)

[Filam]

Et comment ca marche pour la vérification ?

On vérifie avec, par exemple,





Et apres ?