Bonjour,
J'aimerai avoir un petit coup de pouce pour démarrer dans la résolution de ces exercices où il faut montrer que l'affirmation est vraie ou fausse :
1.Soit a : R ->[0 ,+ inf[ une fct C1 qui ne prend que des valeurs positives. Soit f une solution maximale de l'equa diff y' = y² + a(x). Alors f n'est pas définie sur R tout entier.
2. Si la fonction f : R->R est solution de l'equ diffy'=y²y^3 +y, et sif(1)>0 alors f est strict positive et strict croissante.
3. Si la fct f : R ->R est solution de l'equa diff y'= sin(y²-x²)+1/2, et si f(0)=-1, alors x>f(x) pour tout x >= 0
Merci
Equation différentielle
7 messages
- Page 1 sur 1
bonjour,
i)
une technique, c'est , grâce aux hypothèses, d'encadrer la fonction f
par des constantes ou des polynomes et d'obtenir la conclusion
à partir d'inégalités
ii)
autre technique:
si l'expression qui "majore" est le membre de gauche d'une
équation différentielle qui s'intégre, on obtiendra certainement
un résultat en faisant un changement d'inconnue lié à la solution:
par exemple, si on majore
y" < y' + y
on aura envie de poser=z(x) e^{-x})
i)
une technique, c'est , grâce aux hypothèses, d'encadrer la fonction f
par des constantes ou des polynomes et d'obtenir la conclusion
à partir d'inégalités
ii)
autre technique:
si l'expression qui "majore" est le membre de gauche d'une
équation différentielle qui s'intégre, on obtiendra certainement
un résultat en faisant un changement d'inconnue lié à la solution:
par exemple, si on majore
y" < y' + y
on aura envie de poser
bonjour,
la 1. est vraie.
soit tel que
tel que 
Dans un voisinage droit de ,
,  avec h>0
avec h>0
par continuité de y, y est une fonction strictement croissante
et > y_0 > 0)
on réapplique l'argument au point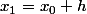
finalement, il existent deux nombres A et B,éventuellement infinis tels que
y est un bijection continue strictement croissante de
 sur
sur 
on peut inverser cette bijection et x est fonctiohn continue, strictement croissante de la quantité y.
L'équa diff. est à variables séparées

en intégrant ces fonctions (continues) de à y ,
à y ,
il vient:

on en déduit que la composante connexe du domaine de définition de y
contenant est bornée supérieurement. Toute solution maximale de l'équation différentielle ne sera jamais définie sur R tout entier.
est bornée supérieurement. Toute solution maximale de l'équation différentielle ne sera jamais définie sur R tout entier.
exemple: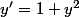
-arctan(y_0))
si , même chose mais cette fois,à gauche de
, même chose mais cette fois,à gauche de  , la fonction
, la fonction  applique
applique
bijectivement, et de manière croissante,
 sur
sur 
Dans ce cas, le domaine de définition de y est borné inférieurement.
la 1. est vraie.
soit
Dans un voisinage droit de
par continuité de y, y est une fonction strictement croissante
et
on réapplique l'argument au point
finalement, il existent deux nombres A et B,éventuellement infinis tels que
y est un bijection continue strictement croissante de
on peut inverser cette bijection et x est fonctiohn continue, strictement croissante de la quantité y.
L'équa diff. est à variables séparées
en intégrant ces fonctions (continues) de
il vient:
on en déduit que la composante connexe du domaine de définition de y
contenant
exemple:
si
bijectivement, et de manière croissante,
Dans ce cas, le domaine de définition de y est borné inférieurement.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
