Suite recurrente majorée

[mateo49]

Bonjour, je bloque toujours sur le même exo :triste:

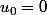
La suite numérique est définie sur N par la donnée et par la relation de récurrence
Pour tout n dans N

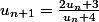
Et la on me demande de montrer que pour tout ,

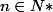
Alors j'ai fait et je trouve mais la je sais pas comment je peux prouver que cette suite obtenu est positive ou négative puisque je connais pas

[LoLLoLLoL]

Etudie f(x)=(2x+3)/(x+4)

[mateo49]

Je ne pense pas que ca soit ca, car en étudiant f(x) je trouve 0< <2 au lieu de 0< <1

[LoLLoLLoL]

Tu peux continuer ce que tu as commencé avec Un+1-1 et montres que |Un+1-1|<|Un-1| et descends la recurrence

[Clu]

La démonstration par récurrence est en effet ce qu'il faut utiliser. Cependant je ne te conseille pas de faire .
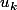
Prouve l'hérédité de la proposition en te posant cette question : si la proposition est vrai pour un certain , est-elle vraie pour ?

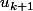
[mateo49]

Je trouve toujours pas!! :cry:
Quelqu'un peu etre plus claire??

[maturin]

alors ce que tu dois montrer c'est la propriété Pn : 00
la récurrence c'est:
- prouve que P1 est vraie
- suppose que Pn est vraie et démontre Pn+1 (avec n>=1)

[Euler07]

Maturin a raison il faut une récurrence

[mateo49]

Sincèrement je trouve toujours pas :triste: , car c'est une suite recurrente et en plus c'est une fraction avec au numérateur et au dénominateur.
Quelqu'un pourrait me montrer le debut du calcule???

[Clu]

Peut-être ne sais-tu pas ce qu'est une démonstration par récurrence ?? Il faut le dire parce-que nous on peut pas savoir.
Je te donne le modèle :

- La proposition à démontrer est la suivante : pour tout , .
- initialisation : cette proposition est-elle vraie pour ?
....

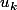
- hérédité : si la proposition est vraie pour un certain , est-elle vraie pour ?
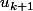
On admet que ,
....
....
....
Donc
- conclusion : d'après le principe de récurrence, la proposition est vraie.

Voilà. La seule difficulté peut résider dans la démonstration de l'hérédité.