soit E l'ensemble des fonctions R+ -> R+ qui vérifient
On note alors
Le problème est de déterminer la borne sup de S(f) lorsque f est dans E.
Optimisation
5 messages
- Page 1 sur 1
Optimisation
par Doraki » 22 Nov 2009, 14:22
Bonjour,
soit E l'ensemble des fonctions R+ -> R+ qui vérifient
dt = 1 \\<br />\bigint_0^\infty f(t)/t dt = 1 \\<br />\bigint_0^1 f(t)/(1-t) dt = 1 \\<br />\bigint_1^\infty f(t)/(t-1) dt = 1)
On note alors = \bigint_0^1 f(t)(t+1) dt + \bigint_1^\infty f(t)(t+1)/t^2 dt)
Le problème est de déterminer la borne sup de S(f) lorsque f est dans E.
soit E l'ensemble des fonctions R+ -> R+ qui vérifient
On note alors
Le problème est de déterminer la borne sup de S(f) lorsque f est dans E.
par Ben314 » 22 Nov 2009, 19:11
Je poserais volontiers =f(t)+{1\over t}f({1\over t}))
pour 
...
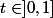
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 22 Nov 2009, 20:39
Aprés moulte calculs (surement faux), je trouve 
(valeur atteinte mais avec une dirac...)
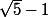
(valeur atteinte mais avec une dirac...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :