Equation correction
33 messages
- Page 1 sur 2 - 1, 2
equation correction
Bonjour pouvez vous m'aider pour cette equation car je n'y arrive pas:
5x^3=8x²
j'ai quand même fais
equivaut à 5x^3-8x²=0
equivaut à 5*x*x*x-8*x*x=0
equivaut à x²(5x-8)=0
pur moi c'est impossible
donc s = ensemble vide
merci d'avance
5x^3=8x²
j'ai quand même fais
equivaut à 5x^3-8x²=0
equivaut à 5*x*x*x-8*x*x=0
equivaut à x²(5x-8)=0
pur moi c'est impossible
donc s = ensemble vide
merci d'avance
Salut,
désolé de te décevoir mais je crois qu'un projet de Loi (une idée, plutôt) est en discussion pour interdire les corrections ... On va bientôt devoir fermer la boutique :/
A part ça, ton polynôme a deux racines (réelles) dont la première est 0 (logique). La deuxième est très simple. Résous simplement ton produit de facteurs nul ... Tu es bien parti.
désolé de te décevoir mais je crois qu'un projet de Loi (une idée, plutôt) est en discussion pour interdire les corrections ... On va bientôt devoir fermer la boutique :/
A part ça, ton polynôme a deux racines (réelles) dont la première est 0 (logique). La deuxième est très simple. Résous simplement ton produit de facteurs nul ... Tu es bien parti.
Bonsoir Timothée tu viens de m'apprendre une nouvelle qui me revolte car beaucoup de personne comme mopi on besoin qu'on les aide moi ce site m'a beaucoup fait progresser et c'est le but de maths-forum et pas comme doivent le penser ceux qui veulent fermer un "site qui fait les devoirs !!"
bon j'en reviens à mon équation :
equivaut à 5x^3-8x²=0
equivaut à 5*x*x*x-8*x*x=0
equivaut à x²(5x-8)=0
equivaut à x²=0 ou x = 8/5
donc S = (0,8/5)
correct ?
bon j'en reviens à mon équation :
equivaut à 5x^3-8x²=0
equivaut à 5*x*x*x-8*x*x=0
equivaut à x²(5x-8)=0
equivaut à x²=0 ou x = 8/5
donc S = (0,8/5)
correct ?
Tu ramènes ton équation du troisième degré à une équation du second degré telle que :
 =
= 
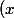(5x^2)) =
= 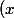(8x))
Tu réduis par :
:
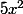 =
= 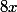
Ensuite tu transpose tous tes termes d'un seul côté de façon à avoir une équation = 0 :
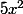 -
- 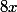 = 0
= 0
C'est alors un polynôme du second degré, tu calcules le discriminant sachant que = B²-4AC :
= B²-4AC :
Tu identifies A; B et C. A = 5; B= -8; et C = 0
 = (-8)² - 4 (5) (0)
= (-8)² - 4 (5) (0)
 = 64 - 4x5x0
= 64 - 4x5x0
 = 64
= 64
 = 8 (car 8² = 64)
= 8 (car 8² = 64)
Tu calcules enfin les deux racines :
x1 =
x1 =-8}{2(5)})
x1 =
x1 =
x1 = 0
x2 =
x2 =+8}{2(5)})
x2 =
x2 =
x2 = 1,6
Voila je t'ai donné les réponses de ton exercice, mais je te conseille vivement d'en refaire car le prochain contrôle, tu peux être sûr d'en avoir, c'est la base...
Je te propose deux exercices pour t'entrainer :
Ex 1:
 +
+ 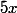 +
+  = -
= -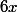 -
- 
Calcule les racines (si il y en a)
Ex 2 :
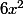 +
+ 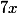 -
- 
Calcule les racines (si il y en a)
Bonne chance
PS : poste tes réponses sur le forum et nous te corrigerons...
Tu réduis par
Ensuite tu transpose tous tes termes d'un seul côté de façon à avoir une équation = 0 :
C'est alors un polynôme du second degré, tu calcules le discriminant sachant que
Tu identifies A; B et C. A = 5; B= -8; et C = 0
Tu calcules enfin les deux racines :
x1 =
x1 =
x1 =
x1 =
x1 = 0
x2 =
x2 =
x2 =
x2 =
x2 = 1,6
Voila je t'ai donné les réponses de ton exercice, mais je te conseille vivement d'en refaire car le prochain contrôle, tu peux être sûr d'en avoir, c'est la base...
Je te propose deux exercices pour t'entrainer :
Ex 1:
Calcule les racines (si il y en a)
Ex 2 :
Calcule les racines (si il y en a)
Bonne chance
PS : poste tes réponses sur le forum et nous te corrigerons...
guiguiflipso a écrit:
Tu réduis par:
Attention ! Réduire par x nécessite x différent de 0 (tes deux équations ne sont pas équivalentes). Tu ne peux diviser par x comme ça.
(Si on appliquait ta méthode, on pourrait dire que
5x^3-8x² = 0 5x-8 =0 x=8/5 ==> il nous manque une solution !!!)
Si tu veux vraiment obtenir ton polynôme du second degré, factorise par x.
m pokora a écrit:Bonsoir guiguiflipso et merci mais je ne comprends pas la presence de Delta etje n'ai jamais vus la regle Delta = = B²-4AC :
je suis en seconde. je vais essayer quand même ton exercice
Je ne te le conseille pas. C'est inutile de faire des exercices sur des théorèmes et propriétés que l'on ne connaît pas. Tu verras cela en 1ère S.
On considère l'équation suivante, où a, b et c désignent des nombres réels et a est différent de 0 :

On dispose de la définition suivante :
Le discriminant de l'équation est la valeur définie par :
définie par :

Si le discriminant est strictement positif, l'équation admet deux solutions x1 et x2 données par les formules suivantes :

Si le discriminant est nul, l'équation n'admet qu'une solution (appelée racine double ):

Si le discriminant est strictement négatif, l'équation n'admet pas de solution réelle.
Tu verras tout cela en 1ère S (c'était mon chapitre préféré d'ailleurs). Tu verras aussi d'où vient ce discriminant. En tout cas ça peut te permettre de résoudre les équations du second degré.
On dispose de la définition suivante :
Le discriminant de l'équation est la valeur
Si le discriminant est strictement positif, l'équation admet deux solutions x1 et x2 données par les formules suivantes :
Si le discriminant est nul, l'équation n'admet qu'une solution (appelée racine double ):
Si le discriminant est strictement négatif, l'équation n'admet pas de solution réelle.
Tu verras tout cela en 1ère S (c'était mon chapitre préféré d'ailleurs). Tu verras aussi d'où vient ce discriminant. En tout cas ça peut te permettre de résoudre les équations du second degré.
Je pense que tu peux expliquer d'où vient le discriminant, il n'y a pas trop de problème à le faire puisque ça résulte d'une simple manip' :)
Le discriminant n'existe pas seulement pour les polynômes de degré deux : par exemple, les polynômes de degré trois ont eux aussi leur discriminant (un peu plus compliqué, il est vrai !).
Au plaisir.
Le discriminant n'existe pas seulement pour les polynômes de degré deux : par exemple, les polynômes de degré trois ont eux aussi leur discriminant (un peu plus compliqué, il est vrai !).
Au plaisir.
guiguiflipso a écrit:Tu ramènes ton équation du troisième degré à une équation du second degré telle que :=

=
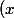(8x))
Tu réduis par:
=
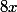
Ensuite tu transpose tous tes termes d'un seul côté de façon à avoir une équation = 0 :-
= 0
C'est alors un polynôme du second degré, tu calcules le discriminant sachant que= B²-4AC :
Tu identifies A; B et C. A = 5; B= -8; et C = 0= (-8)² - 4 (5) (0)
= 64 - 4x5x0
= 64
= 8 (car 8² = 64)
Tu calcules enfin les deux racines :
x1 =
x1 =-8}{2(5)})
x1 =
x1 =
x1 = 0
x2 =
x2 =+8}{2(5)})
x2 =
x2 =
x2 = 1,6
Supers calculs. L'art de se compliquer la vie pour pas grand chose
Tu simplifies par
guiguiflipso a écrit:Voila je t'ai donné les réponses de ton exercice
Hé oui, à l'encontre des règles de ce forum. C'est pour ça que tu es sanctionné.
Mais comme faute avouée est à demi-pardonnée, tu n'es qu'à demi-sanctionné.
Sve@r a écrit:Tu simplifies parce qui donne 5x=8 et la solution est immédiate.
Tu fais la même erreur que guiguiflipso...
Comme cela a été rappelé plusieurs fois dans ce topic (mais j'en remet une couche pour qu'il n'y ai pas de confusion), si tu simplifies par
Pour éviter de se compliquer la vie, c'est la méthode adoptée dès le premier message de m pokora qui est la plus adaptée.
33 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 =
= 
 =
= 
 :
: =
= 