Equation différentielle TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adrien202
- Membre Naturel
- Messages: 84
- Enregistré le: 09 Sep 2007, 17:53
-
 par adrien202 » 21 Nov 2009, 09:54
par adrien202 » 21 Nov 2009, 09:54
bonjour,
j'ai un problème avec la dernière question d'un exo.
a) g(x)= 0,4cos(x)+0,2sin(X)
démontrer que g solution de l'équation y'+2y=cos(x) (E)
Donc celle la, c'est bon.
b) Démontrer que f est solution de (E) si, et seulement si,
f-g est solution de l'équation y'+2y=0
Pareil, là aucun soucis.
c) Résoudre (E)
je ne sait pas par où commencer ni les étapes à suivre.
Pourriez-vous m'aider?
Merci d'avance.
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 21 Nov 2009, 10:04
par annick » 21 Nov 2009, 10:04
Bonjour,
tu sais résoudre y'+2y=0. Donc tu peux trouver f-g. Tu connais g, donc tu peux trouver f.
-
adrien202
- Membre Naturel
- Messages: 84
- Enregistré le: 09 Sep 2007, 17:53
-
 par adrien202 » 21 Nov 2009, 10:18
par adrien202 » 21 Nov 2009, 10:18
oui, mais en fait ce que je n'ai pas compris c'est qu'on nous dit :
montrer que g(x)= 0,4cos(x)+0,2sin(X) solution de (E)
puis on nous demande résoudre (E)
mais la solution de (E) c'est g...
Ou est-ce que f et une autre fonction solution de (E).
Et dans ce cas comment prouver qu'il n'y a pas d'autres solutions?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 21 Nov 2009, 10:57
par annick » 21 Nov 2009, 10:57
g est une solution particulière de (E), mais on cherche une solution f générale. Et on arrive à la déterminer en partant de la solution particulière g.
-
adrien202
- Membre Naturel
- Messages: 84
- Enregistré le: 09 Sep 2007, 17:53
-
 par adrien202 » 21 Nov 2009, 11:38
par adrien202 » 21 Nov 2009, 11:38
f(x) vaut-elle f(x)= x cos(x)+ 0,5x sin(x) ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 21 Nov 2009, 12:30
par Ericovitchi » 21 Nov 2009, 12:30
non, as tu vraiment trouvé la solution de y'+2y=0 ?
-
adrien202
- Membre Naturel
- Messages: 84
- Enregistré le: 09 Sep 2007, 17:53
-
 par adrien202 » 21 Nov 2009, 12:56
par adrien202 » 21 Nov 2009, 12:56
j'ai fait:
f solution de (E) ssi f-g solution de y'+2y=0
je part de f-g solution de y'+2y=0
ssi (f-g)'+2(f-g)=0
ssi f '+2f= g'+2g
ssi f '+2f= cos(x)
ssi f solution de (E)
Est-ce juste?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 21 Nov 2009, 13:01
par Ericovitchi » 21 Nov 2009, 13:01
oui très bien. Restes à trouver f-g solution de y'+2y=0 de laquelle tu déduiras f (puis que tu as déjà g).
Donc tu n'y coupes pas, il te faut résoudre y'+2y=0
-
adrien202
- Membre Naturel
- Messages: 84
- Enregistré le: 09 Sep 2007, 17:53
-
 par adrien202 » 21 Nov 2009, 13:34
par adrien202 » 21 Nov 2009, 13:34
donc j'ai (f-g)= Ce^(-2x) avec C qui appartient à R.
donc f=Ce^(-2x)-g
désolé, il y a un truc que je dois pas comprendre mais je n'arrive toujours pas à trouvé f, ou en l'occurence C

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 21 Nov 2009, 13:37
par Ericovitchi » 21 Nov 2009, 13:37
C'est + g
f=Ce^(-2x)+g donc
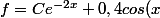+0,2sin(x))
Il n'y a pas à trouver C, tu as trouvé la forme générale de toutes les fonctions qui satisfont ton équation différentielle. Il y en a une infinité, C pouvant prendre n'importe quelle valeur dans R.
-
adrien202
- Membre Naturel
- Messages: 84
- Enregistré le: 09 Sep 2007, 17:53
-
 par adrien202 » 21 Nov 2009, 13:53
par adrien202 » 21 Nov 2009, 13:53
D'accord, j'ai compris!
Merci beaucoup pour votre aide!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
