Suite "imaginative"
25 messages
- Page 2 sur 2 - 1, 2
Une autre méthode consiste effectivement à prendre la suite 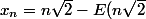) (partie entière).
(partie entière).
Si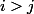 on a alors
on a alors 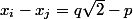 où
où 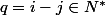 et
et 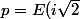-E(j\sqrt{2})\in{\bb Z}) .
.
On peut alors montrer que (je te laisse faire les calculs....)
1) La fraction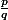 est "assez proche" de
est "assez proche" de  .
.
2) Ici, c'est un peu "vicieux" : en fait il faut montrer qu'aucune fraction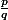 n'approxime "trés trés" bien
n'approxime "trés trés" bien  : Comme
: Comme  n'est pas un quotient, l'entier
n'est pas un quotient, l'entier 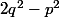 ne peut pas être nul, donc, en valeur absolue, il est supérieur à 1 et cela montre que
ne peut pas être nul, donc, en valeur absolue, il est supérieur à 1 et cela montre que ^2|\ge {1\over q^2}) .
.
3) On en déduit (à toi la main) que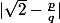 est "assez grand" (il faut utiliser le 1) ici pour majorer
est "assez grand" (il faut utiliser le 1) ici pour majorer 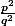 ...) puis que
...) puis que 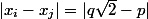 est "assez grand"...
est "assez grand"...
Bon courage (les calculs ne sont pas trés compliqués : c'est l'idée du 2) qui est vicieuse)
Si
On peut alors montrer que (je te laisse faire les calculs....)
1) La fraction
2) Ici, c'est un peu "vicieux" : en fait il faut montrer qu'aucune fraction
3) On en déduit (à toi la main) que
Bon courage (les calculs ne sont pas trés compliqués : c'est l'idée du 2) qui est vicieuse)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Un petite remarque : si tu veux faire le "vicieux", tu peut remplacer le " "
"
par n'importe quel réel "algébrique de degrés 2" (i.e. qui soit racine d'un polynôme de degrés 2 à coefficients dans Z) mais qui ne soit pas un quotient. Par exemple, cela marcherait tout pareil avec le nombre d'or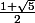 (pour montrer que ce n'est pas un quotient, tu fait tout pareil que pour
(pour montrer que ce n'est pas un quotient, tu fait tout pareil que pour  )...
)...
par n'importe quel réel "algébrique de degrés 2" (i.e. qui soit racine d'un polynôme de degrés 2 à coefficients dans Z) mais qui ne soit pas un quotient. Par exemple, cela marcherait tout pareil avec le nombre d'or
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
