Limites à déterminer
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Flipper81
- Messages: 8
- Enregistré le: 18 Nov 2009, 17:38
-
 par Flipper81 » 18 Nov 2009, 17:43
par Flipper81 » 18 Nov 2009, 17:43
Bonjour à tous,
Voici la limite qu'il me faut résoudre :
}^{\frac{1}{sin(2t)}})
Ma calculatrice m'indique mais
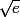
je ne vois pas du tout comment le démontrer.
Merci d'avance de m'aider.
Flipper81
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2009, 17:44
par Nightmare » 18 Nov 2009, 17:44
Salut
Déjà passer à l'exponentielle puis ensuite je dirai un DL même si il doit y avoir plus astucieux !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2009, 17:45
par Nightmare » 18 Nov 2009, 17:45
Effectivement, pas besoin de DL :
sin(2t)=2sin(t)cos(t) et tan(t)=sin(t)/cos(t) ça suffit en utilisant la forme exponentielle :happy3:
-
Flipper81
- Messages: 8
- Enregistré le: 18 Nov 2009, 17:38
-
 par Flipper81 » 19 Nov 2009, 08:57
par Flipper81 » 19 Nov 2009, 08:57
C'est ce que j'ai pensé à faire ; mais tout développement fait j'obtiens :
)^{\frac{1}{sin(2t)}}=\Big( {\frac{(1-i)e^{it}+(1+i)e^{-it}}{e^{it}+e^{-it}}\Big) ^{\frac{2i}{e^{2it}-e^{-2it}}}.)
Et cela ne me lève pas l'indétermination lorsque je fais tendre t vers 0... ou alors je rate quelque chose ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 19 Nov 2009, 14:36
par Pythales » 19 Nov 2009, 14:36
Tu compliques beaucoup.
Soit
^{\frac1{\sin2t}})
\sim\frac{tgt}{\sin2t})
A toi de conclure ...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Nov 2009, 15:04
par barbu23 » 19 Nov 2009, 15:04
Pour ce type de formule, il faut appliquer Un developpement limité simple ! c'est facile à trouver ! :happy2:
-
grikor
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Mai 2009, 16:39
-
 par grikor » 19 Nov 2009, 16:05
par grikor » 19 Nov 2009, 16:05
bonjour,
y=(1+tgt)^((1/sin2t)
lny=ln[(1+tgt)]/sin2t;
lim lny=lim {ln[(1+tgt)]/sin2t}=lim{ln[(1+tgt)]'/(sin2t)'}(reglede L'Ospitale)...
ça donne lim lny=1/2.alors y-->e^(1/2)
-
Flipper81
- Messages: 8
- Enregistré le: 18 Nov 2009, 17:38
-
 par Flipper81 » 20 Nov 2009, 10:53
par Flipper81 » 20 Nov 2009, 10:53
Bonjour,
Merci pour vos réponses, je n'avais pas du tout pensé à utiliser la fonction ln. C'est sûr qu'une fois cette astuce trouvé la suite vient facilement... et on n'est pas d'ailleurs pas obligé d'utiliser la règle de l'hopital (en fait je ne "pouvais" pas l'utiliser ni les DL...)
Merci encore en tout cas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités