Polynomes

[ali babouche]

Salut à tous. Je viens de débuter mon cours sur les polynomes donc je ne suis pas encore très à l'aise. On me demande d'étudier des polynomes dits réciproques (ie ak = a(n-k) où les ak sont les coeff du polynôme.
Soit P = somme de k=0 à n de (a_kX^k).
1) Montrer que 0 n'est pas racine de P (comment fait-on? ) puis montrer que si z est racine de P alors 1/z l'est aussi (idem)
2) Soit n impair, montrer que -1 est racine de P. puis, en notant Q le quotient dans la division euclidienne de P par X+1, montrer que Q est aussi 1 polynome réciproque.
Je souhaite juste que vous m'aidiez à démarrer, car après en ayant compris ça devrait aller mieux. merci par avance

[girdav]

Salut.
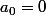
1) Si est racine alors . Mais ne ressemble-t-il pas à un autre coefficient?
2) Ecris ce que vaut puis change d'indice dans la somme .

[Black Jack]

Avec ak = a(n-k), P(x) peut s'écrire :

P(x) = a_n.x^n + a_(n-1).x^(n-1) + a_(n-2).x^(n-2) + ... + a_(n-1).x + a_n

Et a_n est différent de 0 pour un polynome de degré n.

Tu dois maintenant pouvoir répondre à la question 1 ...
********

:zen:

[ali babouche]

1) On a a0 = an. Si 0 racine, alors nécessairement a0=0. Or, P est un polynome de degré n, donc an est différent de 0. Donc par l'absurde 0 n'est pas racine
2) P(-1) = a0 -a1 +a2 +... -an = a0-a1+a2 +... -a2 (=an-2) + a1 (=an-1) - a0 =0 ??Merci en tout cas, une aide pour la suite ?

[ali babouche]

si z racine alors 1/z racine, je ne vois pas. merci de m'aider

[girdav]

Calcule de deux façons: avec la définition directe puis en te servant de ce que tu sais sur les coefficients et d'un changement d'indices dans la somme.

[ali babouche]

j'ai essayé de factoriser par a0, a1 .. sans résultat. Explicites un peu ton changement d'indice stp

[abcd22]

Soit P = somme de k=0 à n de (a_kX^k).
1) Montrer que 0 n'est pas racine de P (comment fait-on? )

Il faut rajouter comme hypothèse que P est non nul sinon c'est faux.

[ali babouche]

merci abcd pour ta précision. Un conseil pour la suite ?

[ali babouche]

avec 1/z, une idée ?

[girdav]

On a .
Si tu comprends ce changement d'indice c'est presque fini.

[ali babouche]

justement je comprends pas ton changement, explicites un peu

[girdav]

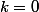
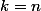
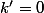
Si je pose , pour on a et pour on a . On passe bien par tous les entiers entre et .

[ali babouche]

en effet, je suis d'accord, mais de là à dire que 1/z est racine..

[girdav]

Après on se sert des propriétés de la puissance.
Met en facteur et tu devrais voir le truc.

[ali babouche]

ça fait (1/z)^n * somme a(n-k) * z^k. or comme z racine de P cela fait zéro. Et ensuite ?