Inéquation exponentielle (term S)

par **ellana69** » 11 Nov 2009, 17:46

Bonsoir,
j'aurais vraiment besoin d'aide pour mon dm de maths s'il vous plait :S j'y ai passé la journée et je commence vraiment à me sentir bête --" lol

Alors voilà jai l'inéquation (1+x)<(ou égal) e^x
je dois en déduire que (1+ 1/n)^n<(ou égal) e

Rien à faire je sèche complètement :hum:
Merci d'avance

par **Dinozzo13** » 11 Nov 2009, 17:49

Salut !
Je trouve ça bizarre, tu passes de termes en

en

?
Si c'est bien ça, pourrais tu me dire dans quel ensemble ils appartiennent.

par **zerkel** » 11 Nov 2009, 17:51

bonsoir,
remplace x par 1/n dans ton inéquation. Et tu seras presque au résultat.

par **ellana69** » 11 Nov 2009, 17:57

oh mon Dieu mais du coup c'est super simple!!! Merci beaucoup
on a donc en posant x=1/n
(1 + 1/n) (1+ 1/n)^n < e en attribuant la puissance n aux deux termes

par **ellana69** » 11 Nov 2009, 18:00

J'ai une autre question du même genre il faut montrer que
e^x<(1/ 1-x) equivaut à e< (1+ 1/n )^n+1

Mais là remplacer x par 1/n ne semble pas marcher :(

par **zerkel** » 11 Nov 2009, 18:14

Pour la première implication essaye avec

.
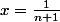
Et pour l'autre ça doit être du même style en faisant bien attention aux intervalles d'appartenance de x et n.

par **ellana69** » 11 Nov 2009, 18:34

non mais j'ai trouvé pour la première question c'est la seconde qui me pose probleme car je trouve en posant x=-1/n
e^-1/n< 1/ (1+ 1/n)
e^-1/n < (1+ 1/n) ^-1
e < (1 + 1/n) ^n or je suis censée trouver e<(1 + 1/n) ^n+1

par **zerkel** » 11 Nov 2009, 18:35

je te parle de la deuxième question (je te précisais juste que cela ne te donnait qu'un sens dans l'équivalence)

par **ellana69** » 11 Nov 2009, 18:40

zerkel a écrit:je te parle de la deuxième question (je te précisais juste que cela ne te donnait qu'un sens dans l'équivalence)

ah d'accord ^^""" euh ben je n'y arrive quand même pas lol

par **zerkel** » 11 Nov 2009, 18:46

tu as remplacé x par

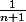
je pense, donc tu es arrivée à

.
Mets au même dénominateur dans le dénominateur de la fraction de droite.
Tu vas donc arriver du

dans la partie gauche de l'inégalité. Et là tu mets n en facteur un numérateur puis tu simplifie.

par **ellana69** » 11 Nov 2009, 18:52

Alors d'abord merci de ta patience lool
mais je trouve e< (1+ 1/n) ^-n-1

par **ellana69** » 11 Nov 2009, 19:43

allo? allo?

par **zerkel** » 11 Nov 2009, 19:46

tu as dû te tromper, parce qu'en théorie tu avais

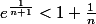
Et là pour obtenir le "e" à gauche tu mets à la puissance (n+1) à droite et à gauche dans l'inégalité.

par **ellana69** » 11 Nov 2009, 19:55

bon je détaille mon calcul:
on pose x=1/ n+1

e^1/n+1< 1/ 1-(1/n+1)
e^1/n+1 < 1/ n/n+1
e^n+1 < 1/ n/n*(1+ 1/n)
e^n+1< (1+ 1/n) ^-1
e < (1+ 1/n) -n-1

par **zerkel** » 11 Nov 2009, 20:04

tu es sensée avoir

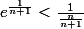
Ce qui te donne:

En mettant n en facteur tu trouves:

par **ellana69** » 11 Nov 2009, 20:07

rolala je suis vraiment fatiguée --"""
Merci beaucoup j'ai compris maintenant

par **zerkel** » 11 Nov 2009, 20:18

ok
tant mieux si tu as compris. Bonne fin de soirée.

par **ellana69** » 11 Nov 2009, 20:38

j'ai une autre question qui me pose problème :cry:
je dois montrer que pour n>ou égal 1 on a 0< e- Un< 4/n
avec Un= (1+n)^n

Alors que trouve très facilement 0 e- Un< 2/n --" (j'e remplace n+1/n par 2/n)

C'est la dernière fois que je demande de l'aide lol

Inéquation exponentielle (term S)

inéquation exponentielle (term S)

Qui est en ligne