[1èreS] DM : Hyperbole et droites

[benekire2]

Oublie l'histoire de la composé... Regarde mon post, il te dit tout sur les variations, j'ai fais ( presque) tout le boulot, on s'en tire très facilement par les simples propriétés de variations, vues en 2nde normalement!!

[Kso]

Merci beaucoup benekire (j'avais pas vu ton post désolée )et jameso ( je suis particulièrement désolée pour Jameso ma nullitée a dû l'accabler, mais je vous promets de faire encore plus d'effort) =) Benekire je vais essayer ça merci ...

[benekire2]

Merci beaucoup benekire (j'avais pas vu ton post désolée )et jameso ( je suis particulièrement désolée pour Jameso ma nullitée a dû l'accabler, mais je vous promets de faire encore plus d'effort) =) Benekire je vais essayer ça merci ...

Tu c'est on peut pas demander a un élève d'utiliser ce qu'il ne maîtrise pas. Déjà qu'il y a des horreurs avec ce qu'ils savent..

Alors de rien, c'était un plaisir, je suppose que ton DM n'est pas terminé, j'ai mis quelques conseils plus haut.

[Kso]

Si tu n'as pas vu la dériv, n'utilise pas cette notion!!

regarde bien comment on en a pas besions:

soit a et b deux nombre de tels que

On a:

or la fonction inverse est décroissante sur donc:


et donc :


Donc f est Décroissante sur cet intervalle, tu fais pareil pour l'autre et tu trouvera décroissant aussi.

Merci de ton soutien moral Benkire =)

Voilà ce que j'ai pu grâce à ton aide :

Soit a et b deux nombres de ]-1 ; + ] tels que -1 <a b.

On a :
-1<a+1b+1 or la fonction est décroissante sur

donc :



et donc :


Donc f est bien décroissante sur cet intervalle mais ce que je ne comprends c'est à la dernière tu as ajouté +1 à la fraction...

[benekire2]

oula excuse moi, je me suis trompé de fonction, dans le principe c'est exactement ca!! Donc, je reprends direct sur:
multiplication par un négatif donc
et donc au final
et voilà du coup la fonction est croissante!!
Complètement désolé, du coup refait la deuxième partie dsl...

[Kso]

Reuuuuh, l'erreur est humaine ne t'inquiète pas ^^
Avant que je ne reprenne ma partie, j'aimerai que tu m'expliques le pourquoi tu multiplies par un négatif (à la deuxième ligne) et pourquoi c'est et pas 2+

Merci d'avance

[Kso]

Reuuuuh, l'erreur est humaine ne t'inquiète pas ^^
Avant que je ne reprenne ma partie, j'aimerai que tu m'expliques le pourquoi tu multiplies par un négatif (à la deuxième ligne) et pourquoi c'est [img]http://www.maths-forum.com/images/latex/74dfeec9ff497ac69c6b69aeb048e4e2.gif[/img et pas 2+[TEX]/frac{1}{a+1}

Merci d'avance

[benekire2]

Reuuuuh, l'erreur est humaine ne t'inquiète pas ^^
Avant que je ne reprenne ma partie, j'aimerai que tu m'expliques le pourquoi tu multiplies par un négatif (à la deuxième ligne) et pourquoi c'est et pas 2+

Merci d'avance

Ben parce que f(a)=2- et non pas 2+ ( ta première question!) enfait, j'ai pris - que l'on a encadrer plus haut puis j'ai simplement ajouter 2 soit -+2 autrement dit 2- :lol5:

[jameso]

Soient x et y deux réels tous les deux différents de -1 tels que x
On a alors x+1
Multiplions par -1 de chaque côté pour obtenir que -1/(x+1)<-1/(y+1) (Je te rappelle que x--->-x est décroissante) ;

il ne reste plus qu'à ajouter 2 de chaque coté pour conclure que f est croissante (stricte) sur tes deux intervalles.

[benekire2]

Soient x et y deux réels tous les deux différents de -1 tels que x-x est décroissante) ;

il ne reste plus qu'à ajouter 2 de chaque coté pour conclure que f est croissante (stricte) sur tes deux intervalles.

Euh ouais, on doit cependant étudier sur les deux intervalles, car 1/x n'est pas continue sur R...

[jameso]

Oui tu as raison ...

[benekire2]

Mais c'est débile, je te l'accorde, un jour, un copain à eu le malheur d'énoncé f(x)=1/x est décroissante sur R* et il s'est fait tuer!! Le prof a mis aucun points sur la question!!

[jameso]

Oui parce ce que c'est faux: j'ai raconté n'importe quoi..


Prends x=-2 et y=2 dans ce cas 1/x=-1/2 et 1/y=1/2 ..... l'ordre est conservé.....bizarre...

C'est la restriction de la fonction inverse à ]-oo,0[ qui est décroissante et la restriction de la fonction inverse à ]0,+oo[ qui est décroissante également

Désolé pour l'erreur...

[benekire2]

Oui parce ce que c'est faux: j'ai raconté n'importe quoi..


Prends x=-2 et y=2 dans ce cas 1/x=-1/2 et 1/y=1/2 ..... l'ordre est conservé.....bizarre...

C'est la restriction de la fonction inverse à ]-oo,0[ qui est décroissante et la restriction de la fonction inverse à ]0,+oo[ qui est décroissante également

Désolé pour l'erreur...

C'est pas grave, parce que, sur ce genre de fonctions, on prend une sale habitude, parce que sur les fonctions inverses composé avec les affines Elles sont de même monotonie sur leurs deux intervalles de définitions... Mais effectivement faut jamais écrire ça...

[Kso]

Merci mille fois !

Donc si je récapitule voilà :

Soit a et b deux nombres de ]-;-1[ tels que ab <-1

On a :

a+1b-1<0 or la fonction inverse est décroissante sur 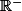donc :



Mais si on multiplies par un négatif, on a donc :


Et donc au final si on ajoute 2 :

2- 2-

Donc la fonction f(x) est croissante sur ]-;-1[.

Soient a et b deux nombres de ]-1;+[ tels que -1<ab.

On a donc : 0 < a+1b+1 or la fonction inverse est décroissante sur 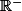donc :


Mais si on multiplie par un négatif on a donc :



et donc au final :
2- 2-

Donc la fonction f(x) est donc croissante sur l'intervalle ]-1;+[

Et voilà,

Pour le tableau de variation, comment fait-on si on n'a pas de courbe ? Certe on connait déjà les intervalles mais qu'écrire sous -1 ?

[benekire2]

Merci mille fois !

Donc si je récapitule voilà :

Soit a et b deux nombres de ]-;-1[ tels que ab <-1

On a :

a+1b-1<0 or la fonction inverse est décroissante sur donc :



Mais si on multiplies par un négatif, on a donc :


Et donc au final si on ajoute 2 :

2- 2-

Donc la fonction f(x) est croissante sur ]-;-1[.

Soient a et b deux nombres de ]-1;+[ tels que -1<ab.

On a donc : 0 < a+1b+1 or la fonction inverse est décroissante sur donc :


Mais si on multiplie par un négatif on a donc :



et donc au final :
2- 2-

Donc la fonction f(x) est donc croissante sur l'intervalle ]-1;+[

Et voilà,

Pour le tableau de variation, comment fait-on si on n'a pas de courbe ? Certe on connait déjà les intervalles mais qu'écrire sous -1 ?

Et bien ca y est de - à -1 croissant et de -1 a croissant, avec la double barre dur le -1 et c'est fini !!

[Kso]

Ah oui, désolée XD j'avais oublié que -1 était exclu, j'avais pas fait aux crochets. Merci.

Mais j'ai, hélas, une autre question, et votre aide est toujours la bienvenue :

3)b) Etudier l'intersection(*) de H avec la droite D:y = x-2, puis D':y=x+1 et enfin D'' : y=x+4.


Moi j'avais pensé :

A calculer le discriminant pour trouver le nombre d'intersection (qui sera forcément 2! ) ...


Et à utiliser f(x) = g(x) (ici D) pour trouver les intersections.

Voilà ce que ça donne :

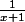2 - = x-2
2 -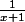 -x+2 = 0

Après le problème c'est que c'est pas évident de trouver le discriminant avec ça... Help ?

(*) Etudier l'intersection de H et D signifie déterminer le nombre de point d'intersection de H et D puis déterminer les coordonnées de ces points lorqu'ils existent.

[Kso]

Paqueté, étiqueté, finish, pour cette question...Merci quand même.

[Kso]

Rebonjour voilà je voulais être sûre de mon résultat et un petit "oui, c'est bon" me suffirait amplement :

2 - - (x-2) = 0 } x+1
=2x+2-1 - (x²+x-2x-2) = 0
=2x+1 - x² -x +2x + 2
=-x² + 3x +3
= b² -4ac
= 3² - 4*(-1)*3
=9+12
=21

Puisque > 0 alors

X1 =

X2=

Et ce srait pas mal aussi si vous me proposiez une échelle pour tracer l'hyperbole de cette fonction
f(x) =

Merci d'avance