Bonsoir,
Quelqu'un pourrait me donner une piste pour démontrer la transformée de fourier après contraction du domaine, c'est a dire :
F{ x(kt) } = 1/k X(w/k)
Merci d'avance
Contraction transformée de fourier
6 messages
- Page 1 sur 1
par fatal_error » 04 Nov 2009, 21:19
salut
Pour calculer))
tu fais
e^{wt} dt)
On peut poser
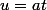
soit
e^{w_2u} du\\<br />\frac{1}{a} \int x(u)e^{w_2 u} du)
avec
soit
) = \frac{1}{a} \int x(u) e^{\frac{w}{a}u} du = \frac{1}{a}X( \frac{w}{a}))
qqch dans le genre
Pour calculer
On peut poser
soit
avec
soit
qqch dans le genre
la vie est une fête 
par Miko95 » 05 Nov 2009, 06:09
Merci pour la réponse,
Pour la deuxieme ligne , ca devrait pas plutot etre e^{jwt} dt)
.
Aussi, pourquoi ne pas mettre
au lieu de seulement t au niveau de la puissance de l'exponentielle, de sorte à avoir e^{jwat} dt)
.
Aussi, je n'ai pas compris c'est quoi le petit 2 au niveau de
e^{w_2u} du\\)
e^{w_2 u} du)
.
Pour la deuxieme ligne
Aussi, pourquoi ne pas mettre
Aussi, je n'ai pas compris c'est quoi le petit 2 au niveau de
par fatal_error » 05 Nov 2009, 07:41
alors l'oubli du j, c'est que je me rappèle pas trop de la TF.
Par contre le a, faut pas qu'il soit en exposant.
Ta fonction)
, c'est comme si t'avais une fonction )
.
Si tu as ta fonction tu as simplement lexponentielle 
le
, parce qu'on a posé 
cad 
Par contre le a, faut pas qu'il soit en exposant.
Ta fonction
Si tu as ta fonction
le
la vie est une fête
par Miko95 » 05 Nov 2009, 08:00
Merci, juste une derniere question, à cette ligne , sachant que
F{x(t)} = X(w), comment sait-on que e^{\frac{w}{a}u} du = X( \frac{w}{a}))
?
F{x(t)} = X(w), comment sait-on que
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :