Congruence et somme

par **variobike01** » 04 Nov 2009, 08:02

Bonjour,

Je bloque sur un exercice d'arithmétique dès le début.

"Pour tout entier naturel

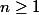
, on pose :

1)a) Démontrez que:

Si

alors

Ce que j'ai fait:

Je me suis aventuré dans le calcul de la somme des terme de Un, mais sans succès.
J'ai trouvé Sn=

=

Mais cette somme me semble bizarre ...

Pouvez vous me dire si c'est la bonne ?

Merci

@+

par **variobike01** » 04 Nov 2009, 08:26

Je viens de me rendre compte d'une erreur, la somme à utiliser est celle d'une suite géométrique et non celle d'une suite arithmétique. :zen:

On a alors: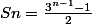

Et ça semble plutôt aller dans le sens de l'exercice contrairement à l'autre suite... :marteau:

par **benekire2** » 04 Nov 2009, 09:09

Eh bien ou est le problème maintenant? ?

par **dudumath** » 04 Nov 2009, 09:21

tu t'es trompé par contre, c'est

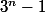
et non pas

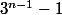
au numérateur

avec ça, c'est fini

par **benekire2** » 04 Nov 2009, 09:23

si a/2 est divisible par 7 alors a est divisible par 7 également...

par **variobike01** » 04 Nov 2009, 09:53

Merci pour l'erreur au numérateur. :marteau:

La où j'ai du mal c'est avec les congruences, je n'arrive pas bien à cerner ce qu'il faut faire.
Je vais essayer de trouver une piste et je reviens vous écrire ce que j'ai trouvé.

En tout cas merci :zen:

par **benekire2** » 04 Nov 2009, 10:26

Oui il faut chercher un peu plus c'est sur...
Fais nous part de tes autres questions!!

par **variobike01** » 04 Nov 2009, 11:40

Voila ce que j'ai trouvé:

On a donc:

On sait également que:

On en conclut que:

Or

ce qui fait:

Voila ce que j'ai trouvé, mais après je ne sais pas si c'est ça ... Même si ça me semble pas trop mal :ptdr:

par **variobike01** » 04 Nov 2009, 15:16

Voila, j'ai encore complété un petit peu l'exercice:

Voici la question 1)b):

Réciproquement, démontrez que:

Si

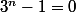
alors

Voici maintenant ce que j'ai fait pour cette partie:

Si

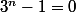
alors

Or

donc

car

.

Il me demande maintenant, à partir de ce résultat, et d'un tableau de congruence, de déduire que

...
Je ne vois pas bien ce qu'est un tableau de congruence.

par **benekire2** » 04 Nov 2009, 15:19

variobike01 a écrit:Voila ce que j'ai trouvé:

On a donc:

On sait également que:

On en conclut que:

Or

ce qui fait:

Voila ce que j'ai trouvé, mais après je ne sais pas si c'est ça ... Même si ça me semble pas trop mal :ptdr:

Te complique pas la vie, la réponse a été donnée avant...

par **dudumath** » 04 Nov 2009, 15:50

variobike01 a écrit:[

Or

:

2*2^n= 4^n ??? j'en doute fort...

par **benekire2** » 04 Nov 2009, 15:52

2*2^n=2^(n+1)

Congruence et somme

Congruence et somme

Qui est en ligne