Classe de conjugaison

par **zz6918** » 02 Nov 2009, 17:39

Bonjour,

préalablement, dans mon exercice j' ai déjà démontrer que G posséde un élément g1 d'ordre 3 et un élément h d' ordre 2
J' ai ensuite montrer que g1 et h engendrent G et que g1 et h ne commutent pas.

soit g2=hg1h-1 et g3=hg2h-1

J' ai montrer que g1 g2 g3 sont deux à deux distincts et que G={e,h,h²,g1,g2,g3}

Maintenant il faut que je démontre que A={g1,g2,g3} est une classe de conjugaison de G et que A engendre G.

Et je ne vois pas du tout comment faire..

Merci

par **yos** » 02 Nov 2009, 21:26

Par définition de

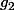
, il est conjugué à

;
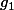
Par définition de

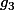
, il est conjugué à

.
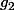
Donc

sont dans la même classe de conjugaison. Reste à montrer qu'il n'y a qu'eux dans cette classe. Tu peux le faire à la main en cherchant tous les conjugués de ces trois éléments.

par **zz6918** » 02 Nov 2009, 23:08

ok pour la classe de conjugaison.
Mais maintenant je ne vois pas comment montrer que A engendre G

par **yos** » 03 Nov 2009, 06:15

T'as juste à fabriquer h avec

.
Ou, plus rapide, et si tu as des notions sur les groupes, tu dis que A engendre un sous-groupe de G d'ordre au moins 4 (

et le neutre) donc d'ordre 6 car l'ordre d'un ssg divise l'ordre du groupe.

par **yos** » 03 Nov 2009, 06:19

zz6918 a écrit:j' ai déjà démontrer que G posséde un élément g1 d'ordre 3 et un élément h d' ordre 2

c'est le contraire non?

par **zz6918** » 03 Nov 2009, 16:49

yos a écrit:c'est le contraire non?

euh non c' est bien ça.. g1 est d' ordre 3

par **zz6918** » 03 Nov 2009, 16:52

yos a écrit:tu dis que A engendre un sous-groupe de G d'ordre au moins 4 ( et le neutre) donc d'ordre 6 car l'ordre d'un ssg divise l'ordre du groupe.

mais si je pose un sous groupe d'ordre 4, ce sous groupe ne divise pas G. car 4 divise pas 6???

par **yos** » 03 Nov 2009, 17:36

zz6918 a écrit:euh non c' est bien ça.. g1 est d' ordre 3

Et h d'ordre 2? Alors que fait ton h² dans le groupe??
Non, il y a un bug dans les infos que tu donnes.

par **zz6918** » 03 Nov 2009, 17:43

yos a écrit:Et h d'ordre 2? Alors que fait ton h² dans le groupe??
Non, il y a un bug dans les infos que tu donnes.

autant pour moi, je me suis trompé..
h est bien d' ordre 3

par **yos** » 03 Nov 2009, 17:47

Connais-tu ce théorème :

yos a écrit:l'ordre d'un ssg divise l'ordre du groupe.

??

par **zz6918** » 03 Nov 2009, 17:57

Lagrange???

par **zz6918** » 03 Nov 2009, 17:58

Lagrange??

par **yos** » 03 Nov 2009, 18:02

Yes.
Alors je répète ce que j'ai dit avant :
Soit H le sous-groupe engendré par A. H contient A , mais aussi e, donc H contient au moins 4 éléments. Peut-il en contenir 4? 5?

...

par **zz6918** » 03 Nov 2009, 18:09

D' aprés Lagrange non,il peut contenir 2 ou 3 élément..

par **yos** » 03 Nov 2009, 20:29

Bon je renonce.

Classe de conjugaison

classe de conjugaison

Qui est en ligne