Forme indeterminée EXP

[mydoudouitsk]

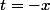
Bonjour,je suis en term S et je cherche la limite en et en de la fonction . J'ai essayé de factoriser par ou en posant mais il semble que cela ne fontionne pas. Je ne trouve donc aucune des deux limites.
Pourriez vous m'aider?

ps: dsl s'il ecrit "en f(x)= x²" le mode prévisualiser m'écrit ça, en réalité ça devrait écrire + l'inf. (pourtant j'ai bien écrit -/infty avec les tex.)

[kushiki]

Bonsoir,

factorise plutot par le x dont la puissance est la plus élevée et ensuite ca devrait marcher. Tu reconnaîtras certaines formules de ton cours.

[mydoudouitsk]

j'ai essayé de factoriser par x mais dans le membre de droite de la factorisation j'obtiens des + l'inf et un - l'inf (donné par - l'inf ) a additionner, ce qui me donne toujours une valeurs interdite.

en factorisant par x:

[kushiki]

il faut plutot factoriser par x² et non pas par x.

tu auras ainsi