Tableau de variations

[Hey-DJ]

Bonjour, j'aurais besoin d'un petit coup de main svp.

Je dois chercher la dérivée de
J'ai trouvé : Est-ce juste ?

Ensuite, je dois faire le tableau de variations :

f'(x)=0
=0
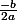
Une seule solution : x=1 ( car =1 )

f(x) sera décroissante pour tout x dans mon tableau. Est-ce juste ?

Merci de m'aider.

[dudumath]

ta dérivée est juste.

Pour le reste, attention:

Il y a une valeur (x=1) pour laquelle f n'est pas définie

tu auras donc, comme ta dérivée est négative sur ]-oo,1[ u ]1,+oo[

f va être décroissante sur ]-oo,1[ et décroissante sur ]1,+oo[

Il faut que tu calcules les limites en 1+ et 1-, ce qui n'est pas très dur

[Hey-DJ]

Ces limites que je dois calculer en 1- et 1+ complètent le tableau de variations c'est bien ça ?

Et sinon je dois calculer le point d'intersection A de la courbe f avec l'axe des abscisses. Comment faire ?

[Hey-DJ]

Svp soyez cool =(

[benekire2]

Tu n'as pas vraiment besoin de tout ça, si tu veut les variations de f, il suffit d'étudier bêtement le signe de f' qui est très simple a étudier.

Dans le tableau tu met -5 négatif tout le long, (x-1) négatif avant 1 et positif après et tu remet x+1 , et le tour est joué