Quelques questions en analyse

[benj38330]

Bonjour à toi aussi !!

Voici quelques questions qui me posent problèmes:

1/ £ u' e^ -u = -e^-u + C ?? es-ce que cette formule est juste??? (£ signifit intégrale)

2/ j'ai £ e^(-Lt)= (e^(-Lt))/ -L . comment trouve t'on ce résultat?? il y a t'il une formule qui existe du genre £ e^(Cx) = (e^Cx)/C , avec C un entier??

3/ Je dois trouver le DLn(0) e^(-x^2/2L^2) .
J'ai changé de variable avec u= (-x^2/2L^2) on a donc DLn(0) e^u a trouver!
J'ai la formule du DLn(0) de e^x mais comment trouver celui de u=(-x^2/2L^2).

Ce que j'ai commencé a faire : j'ai dérivée plusieurs fois u et j'ai trouver u'= - x/L^2 ,u'' = -1/L^2 puis u''' = 0 Pour cela j'ai considéré que L est un nombre entier. Et maintenant je ne sais plus quoi faire...

Es-ce que quelqu'un pourrais m'aider à continuer dans cet exercice??? et Répondre à mes 2 premières questions??

Merci d'avance :help:

[Ericovitchi]

oui car u'dx c'est du et la primitive de c'est bien


c'est donc un et la primitive est donc


ca veut dire quoi : le DLn ? écris mieux tes formules.

[benj38330]

Tout d'abord merci pour ces réponses!! ça m'aide pas mal à comprendre

sinon pour le 3/ Ce qui m'est demandé c'est le developpement limité d'ordre n de e^(-x^2/ 2 L^2) en 0 .

Au passage si quelqu'un à peut m'expliquer comment faire un développement limité d'une fonction??? ( es-ce que l'on calcule les dérivées successive jusqu'a ce qu'on arrive à une formule générale??? ou es-ce que c'est autrement)
Ici dans mon exemple j'ai utilisé le dévéloppement limité d'une fonction composé... j'ai donc la formule de dévéloppement limité de e^u mais pas celle de l'autre fonction (-x^2/ 2 L^2). Comment l'obtenir et puis comment la remettre en lien avec e^u.


(Dsl pour la non clarté de mes formule mais je ne sais pas comment bien les écrires comme dans les réponses des différents membres)

[Ericovitchi]

La page de wikipedia sur les développements limités te donne toutes les explications : http://fr.wikipedia.org/wiki/D%C3%A9veloppement_limit%C3%A9

Pour calculer le tien tu pars de celui de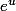
et puis tu remplaces u par

[benj38330]

Bonjour merci pour le lien.

Je suis allé voir et ils donnent en exemple le DL de e^(1/1-x)

et pour avoir son DL ils trouvent celui de exp puis celui de 1/1-x.

j'aimerais savoir comment ils font pour trouver celui de 1/1-x et plus particulièrement dans mon cas celui de (-x^2/ 2 L^2).

Sinon toi tu pense que juste en remplacant u par sa valeur , c'est bon???
ça me prait un peu facile par rapport a l'exemple donné. Dans leurs cas ils auraient du avoir alors e^(1/1-x)= 1+(1/1-x)+... et ce n'est pas le cas.

Peut tu m'éclaircir la dessus parce que avec les formules données le DL en général n'est pas clair pour moi.

Merci

[Ericovitchi]

Effectivement dans le cas présent tu peux faire ce que j'ai dit uniquement parce que (-x^2/ 2 L^2) est déjà son propre développement limité. On peut donc remplacer bêtement.

Mais si tu avais une fonction comme 1/(1-x) ou sinx il faudrait effectivement en faire aussi le développement limité
1/(1-x)=1+x+x²+ .... , prendre un certain nombre de termes et les remplacer dans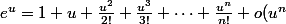 puis regrouper les termes en x, x², etc...
C'est assez long et il n'y a pas de formule générique du coup.