Exercice: dérivée de fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 15:26
par tim39 » 30 Oct 2009, 15:26
Bonjour,
Je ne me souviens plus de quelle manière l'on dérive ce type de fonction:
= (3(x+10)^2)/(x^2+400))
Je penses que f(x) est de la forme
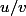
avec:
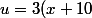^2)
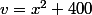
Pourriez-vous m'aider a trouver la dérivée de cette fonction?
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 15:31
par jameso » 30 Oct 2009, 15:31
Regarde dans ton cours la formule de dérivation d'un quotient...
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 15:33
par tim39 » 30 Oct 2009, 15:33
je la connais par cur =>

-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 15:39
par tim39 » 30 Oct 2009, 15:39
j'avais déjà essayé et ça me donnai,
2)
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 15:40
par tim39 » 30 Oct 2009, 15:40
La fonction est donc croissante sur R? pouvez-vous confirmer?
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 15:52
par jameso » 30 Oct 2009, 15:52
Tu as fais une erreur de calcul au numérateur: tu dois trouver au numérateur 60(x+10)(40-x)
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 16:18
par tim39 » 30 Oct 2009, 16:18
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 16:36
par jameso » 30 Oct 2009, 16:36
Avant de penser à dériver, je te fais remarquer que (x+10)² n'est pas égal à x²+100 (tu oublies le double produit....) Tu es en quelle classe ?
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 16:54
par tim39 » 30 Oct 2009, 16:54
Oui désolé, ça peut arriver à tout le monde...
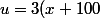^2=3(x^2+20x+10^2)=3x^2+60x+300)
Donc u'=60x+60=60(x+1)
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 17:03
par jameso » 30 Oct 2009, 17:03
La dérivée de 3x² est 6x et non 60x...
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 17:07
par tim39 » 30 Oct 2009, 17:07
Oui c'est ce que j'avais noté sur ma feuille.
Donc u'=6x+60=6(x+10)
Merci de prendre du temps pour m'aider c'est très gentil
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 17:14
par tim39 » 30 Oct 2009, 17:14
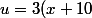^2)
ou

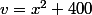
u'=6(x+10)
v'=x^2+400
je n'arrive pas à amorcer le calcul:
=[6(x+10)(x^2+400)-(2x)(3(x+10)^2)] / (x^2+400)^2)
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 17:14
par jameso » 30 Oct 2009, 17:14
C'est bien parti .. pense maintenant à factoriser le numérateur (toujours penser à factoriser les derivées..)
-
tim39
- Membre Naturel
- Messages: 21
- Enregistré le: 03 Fév 2008, 18:45
-
 par tim39 » 30 Oct 2009, 17:47
par tim39 » 30 Oct 2009, 17:47
Après développement je trouve:
=[60(-x^2+30x+400)]/(x^2+400)^2)
=60(x+10)(40-x)/(x^2+400)^2)
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 18:19
par jameso » 30 Oct 2009, 18:19
J'ai trouvé la même chose...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 103 invités