Exercice sur la fonction exponentielle

[Falanaka]

Bonjour à tous,
je vous expose une question que je n'arrive pas à résoudre:
En utilisant le résultat lorsque h tend vers l'infini positif alors (1+1/h)^h = e, établir que:
lorsque p tend vers l'infini positif alors C*(1+i/p)^(pn)=C*e^(in).
Dans cette question je ne vois pas comment i se retrouve en puissance or c'est la clé de l'exercice. Je vous remercie d'avance pour vos conseils,
Falanaka

[MacManus]

Bonjour

Moi j'aurais dis plutôt

[Falanaka]

Non, j'ai bien écrit l'équation, n n'est pas au numérateur mais bien à la puissance pour le premier membre. D'ailleurs il me semble assez logique que si il est à la puissance dans le premier membre il le reste pour le second. Ce que je comprend moins bien c'est que i soit au numérateur pour le premier et qu'il passe à la puissance pour le second...

[Falanaka]

Voici l'équation. Ici C n'est pas une fonction.

[MacManus]

Oui d'accord j'ai dû brûler 1 étape :

en fait, tu peux écrire que , or d'après ta formule
(ton "e" ici n'est pas la fonction exponentielle, mais le nombre e 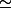2,72), donc et ton i est bien en exposant (mais attention, signifie bien exponentielle de i), et donc

------------------------------------------------------

Sinon tu peux écrire que et raisonner par équivalents, c'est plus subtile et ce n'est pas au programme au lycée...mais bon pas de panique , en utilisant le fait que log(1+u)~u lorsque u tend vers 0 (lire log(1+u) équivaut à u lorsque u tend vers 0), ici si l'on pose 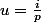, alors 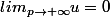et on peut donc appliquer cette formule pour les équivalents, c'est-à-dire que ~lorsque , on peut donc écrire que :

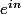~~. On a donc tous ces équivalents lorsque p tend vers + biensûr. Enfin, multiplier par la constante C ne modifie pas le résultat.

Voilà j'espère ne pas dire de bêtises au sujet des équivalents pour les exponentielles, je me méfie...