Résoudre dans les entiers relatifs :
C'est pas très difficile mais bon ^^
Equation diophantienne
4 messages
- Page 1 sur 1
Equation diophantienne
par Asymetric » 15 Oct 2009, 19:06
Bonjour,
Résoudre dans les entiers relatifs :\frac{y}{x} + 1}{(x^2 - y^2)\frac{y}{x} - 1})
.
C'est pas très difficile mais bon ^^
Résoudre dans les entiers relatifs :
C'est pas très difficile mais bon ^^
par Matt_01 » 28 Oct 2009, 13:59
Par une méthode un peu "moche", je trouve que les seules solutions sont (-d,d) avec d dans Z*. C'est ça ?
par Matt_01 » 28 Oct 2009, 14:25
Bon alors voilà ma méthode :
On écrit
et 
avec 
et 
premiers entre eux. On prend 
(S'il était négatif on aurait juste à prendre -d à la place de d)
En effectuant le produit en croix (et en ayant multiplié par x aux deux membres de la fraction auparavant) on a :
d \beta -d \alpha) =<br />\beta d (d^2(\alpha^2-\beta^2)d \beta +d \alpha))
En factorisant par
non nul on a :
 \beta - \alpha) =<br />\beta (d^2(\alpha^2-\beta^2) \beta + \alpha))
En raisonnant modulo, on a divisible par et donc 
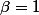
(ils sont premiers entre eux)
On obtient :
 -\alpha) = (d^2(\alpha^2-1) +\alpha)
On factorise par
:
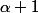
(\alpha d^2(\alpha -1))=(\alpha +1)(d^2 (\alpha -1) + \alpha))
Ce qui fournit
ou =d^2 (\alpha -1) + \alpha)
La deuxième équation n'a pas de solution (on peut s'en persuader modulo, ce qui donne 
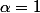
qui n'est pas solution)
Finalement
et 
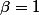
ce qui fournit 
et 
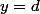
qui sont bien solutions du problème.
On écrit
En effectuant le produit en croix (et en ayant multiplié par x aux deux membres de la fraction auparavant) on a :
En factorisant par
En raisonnant modulo
On obtient :
On factorise par
Ce qui fournit
La deuxième équation n'a pas de solution (on peut s'en persuader modulo
Finalement
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :