Une urne contient 6 boules : 4 rouges et 2 noires.
1.On tire 2 boules de l'urne sans remise. Calculer la probabilités des événements suivants:
a) A : On n'a obtenu aucune boule noire
b) A' : On a obtenu une seule boule noire
c) A'' : On a obtenu deux boules noires
2.Apres ce 1er tirage, il reste 4 boules dans l'urne et on tire à nouveau 2 boules de l'urne sans remise.
On note B0 : On n'a obtenu aucune boule noire au deuxième tirage
On note B1 : On a obtenu une seule boule noire au deuxième tirage
On note B2 : On a obtenu deux boules noires au deuxième tirage
a) Calculer
 P_{A'}(B0) et P_{A''}(B0))
. Calculer P(B0).
b)Caluler la probabilité de P(B1) et P(B2)
1. L'univers
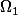
est les combinaisons de deux boules parmi les 6 de l'urne soit
= \left(6\\2\right).)
 = \left(4\\2\right))
car on choisit deux boules rouges parmi les 4 de l'urne
 = 2 \times 4)
car il y a 2 possibilité pour tirer une boule rouge puis 4 possibilité de tirer un boule rouge pour compléter le tirage.
 = 1)
car il y a une seule possibilité d'obetenir deux boules noires.
2. On considère l'univers
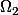
l'emsembles des combinaisons de 2 boules parmi les 4 de l'urne. On a
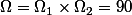
card (A

B0) =
 \times 1)
car il y a
)
façons de tirer deux boules rouges au premier tirage et 1 façon de tirer deux boules rouges au deuxième tirage.
P(A

B0)=
} {90})
card (A'

B0) =
)
car il y a 8 façons de tirer une seule boule noire au premier tirage puis
)
façons de tirer deux boules rouges au deuxième tirage.
P(A'

B0) =
} {90})
card (A''

B0) =
)
car il y a une seule possibilité pour tirer 2 boules noires au premier tirage et
)
façons de tirer de 2 boules rouges au deuxième tirage.
P(A''

B0)=
}{90})
Est-ce juste? Comment calculer P(B0), P(B1) et P(B2)? Merci.
