Résidus quadratiques

[gilles3]

Bonjour,
j'ai besoin d'un peu d'aide sur cet exercice

Soit:




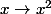
est premier impair

Si l'équation possède une solution alors elle en a exactement deux et .

Il est évident que (par définition de ).

Ce que je veux montrer, c'est qu'il en n'existe que 2 et 2 seulement (au maximum).

et je ne vois pas trop comment faire:dois ton supposer l'existence d'une 3e solution, et qu'on aboutirait à une contradiction?

[Nightmare]

Salut !

Eh bien, si y est une solution :

x²=a <=> (x-y)(x+y)=0 et vu qu'on est dans un anneau intègre cela implique que x=y ou x=-y !

On a donc au mieux deux solutions.

[gilles3]

ah oui, je ne connaissais pas cette propriété, mais en tout cas, elle est très utile.
merci beaucoup

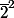
Mais j'ai aussi une autre question: je dois montrer que les classes d'équivalences , , ...., dont distincts deux à deux.

et là j'ai pas trop d'idée.

[Nightmare]

As-tu réfléchis à ce qu'on te demande? C'est une application directe de ce que tu as trouvé avant !

On sait qu'au maximum deux classes peuvent être égales, et on sait de plus que si une classe x est solution, la deuxième est p-x. En particulier si x est dans {1,...,(p-1)/2}, la deuxième solution est dans {p/2,...,p}. Donc tous les x² avec x dans {1,...,(p-1)/2} sont distincts.

[fourize]

salut tout le monde !

Salut !
x²=a (x-y)(x+y)=0 .

au passage Nightmare! tu pourrais expliquer comment on arrive à ça !?
je pensais premierement que :
x²= a x²-a = 0 (pas possible d'arriver à (x-y)(x+y)=0

deuxiemement je pensais:
(x-y)(x+y) =0 x² - y² =0 x²=y² ?? mais que ce qui dit que y²=a ???

merci !

[Nightmare]

Salut !

J'ai posé y comme vérifiant y²=a !

Donc si on a aussi x²=a, x²-y²=0 d'où comme je l'ai écrit x=y ou x=-y donc au mieux deux solutions, opposées.

[fourize]

Salut !
J'ai posé y comme vérifiant y²=a !
Donc si on a aussi x²=a, x²-y²=0 d'où comme je l'ai écrit x=y ou x=-y donc au mieux deux solutions, opposées.

merci de ta precision, pourtant j'avais bien lu que ta supposer y etant solution ! :dodo: peut etre :dodo: mmmmmmmerrrrrrrcccccccciiiii encore !