Fonction usuelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lala1
- Membre Naturel
- Messages: 75
- Enregistré le: 12 Mai 2007, 15:59
-
 par lala1 » 18 Oct 2009, 15:39
par lala1 » 18 Oct 2009, 15:39
bonjour,
je ne sais pas comment faire pour démontrer la relation suivante, pouvez vous me donner une piste s'il vous plait,
pour tout x appartenant à ]0,1] arctanracine((1-x²)/ x²) = arccosx
merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Oct 2009, 15:40
par Nightmare » 18 Oct 2009, 15:40
Salut !
Une méthode consiste par exemple à poser x=cos(u), le membre de droite vaut u, celui de gauche vaut...
Une autre méthode consiste à montrer que les dérivées des deux membres sont égales (un peu plus long)
-
lala1
- Membre Naturel
- Messages: 75
- Enregistré le: 12 Mai 2007, 15:59
-
 par lala1 » 18 Oct 2009, 16:53
par lala1 » 18 Oct 2009, 16:53
merci je vais essayer
-
lala1
- Membre Naturel
- Messages: 75
- Enregistré le: 12 Mai 2007, 15:59
-
 par lala1 » 18 Oct 2009, 17:56
par lala1 » 18 Oct 2009, 17:56
je ne sais pas du tout comment faire pour simplifier après avoir remplacer x par cos(u)...
je vais essayer la deuxième méthode pour voir...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Oct 2009, 17:57
par Nightmare » 18 Oct 2009, 17:57
Que vaut 1-cos²(u) ?
-
lala1
- Membre Naturel
- Messages: 75
- Enregistré le: 12 Mai 2007, 15:59
-
 par lala1 » 18 Oct 2009, 17:59
par lala1 » 18 Oct 2009, 17:59
cela vaut sin²(u)
-
lala1
- Membre Naturel
- Messages: 75
- Enregistré le: 12 Mai 2007, 15:59
-
 par lala1 » 18 Oct 2009, 18:05
par lala1 » 18 Oct 2009, 18:05
ensuite alors on enlève la racine et on a
arctan sin²(u)/ cos²(u) = u²
puis comme tan=sin(u)/cos(u)
alors arctan=tan(u)*(sin(u)/cos(u))= u
-
lala1
- Membre Naturel
- Messages: 75
- Enregistré le: 12 Mai 2007, 15:59
-
 par lala1 » 18 Oct 2009, 18:26
par lala1 » 18 Oct 2009, 18:26
je ne sais pas du tout comment montrer la relation, j'ai en fait du mal à utiliser les arccos et arctan
je confond avec cosx et tanx.
comment peut on savoir combien fait arccosx parce que vous m'aviez dit que c'était égale à x mais pourquoi?
je ne vois pas quelle formule utilisée
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 18 Oct 2009, 19:44
par wserdx » 18 Oct 2009, 19:44
Peut-être que ceci va t'aider.
Prends l'exemple
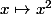
et
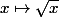
Ces deux fonctions sont réciproques l'une de l'autre.
On a pour tout

,

De même pour

et

On a pour tout

,

) = x)
et pour tout

,

,
) = x)
La petite difficulté c'est de bien trouver l'ensemble de définition de la fonction réciproque, mais ce n'est pas insurmontable...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
