Equation à nouveau
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Malamat
- Membre Relatif
- Messages: 107
- Enregistré le: 03 Oct 2009, 13:36
-
 par Malamat » 16 Oct 2009, 17:18
par Malamat » 16 Oct 2009, 17:18
Bonsoir,
J'ai des difficultés à comprendre comment on peut passer des équations (1)
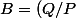 C)
et (2)

à la valeur de

qui est la suivante :

En remplaçant (2) dans (1), je trouve en effet

et non pas

Pourriez-vous m'aider ? :help:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 16 Oct 2009, 17:35
par Ericovitchi » 16 Oct 2009, 17:35
tout simple, tu multiplies les deux équations (1) et (2) membre à membre.
-
Malamat
- Membre Relatif
- Messages: 107
- Enregistré le: 03 Oct 2009, 13:36
-
 par Malamat » 16 Oct 2009, 17:50
par Malamat » 16 Oct 2009, 17:50
Merci pour votre réponse, Ericovitchi :happy3:
Cela dit je viens d'essayer la multiplication membre à membre, je trouve ceci :
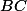
=
 C])
*
)
Ce qui me donne ensuite :
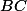
=

Pour finir par

, comme tout à l'heure.
Je ne vois pas où je pourrais avoir fait une erreur :triste:
-
Malamat
- Membre Relatif
- Messages: 107
- Enregistré le: 03 Oct 2009, 13:36
-
 par Malamat » 16 Oct 2009, 18:08
par Malamat » 16 Oct 2009, 18:08
Est-ce mon énoncé qui est faux ?
-
enjolras
- Membre Naturel
- Messages: 55
- Enregistré le: 15 Oct 2009, 14:36
-
 par enjolras » 16 Oct 2009, 19:44
par enjolras » 16 Oct 2009, 19:44
il me semble que tu fais une confusion entre 2q et Q²
en outre ultiplier les deux inégalités ne me semble pas etre la meilleurs solution...
qu'est ce qui permettrait de supposer c non nul ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 16 Oct 2009, 20:44
par Ericovitchi » 16 Oct 2009, 20:44
non, BC = [(Q/P) C] * (R/2Q) ça va, mais après ça cloche
tu multiplies mal les numérateurs et les dénominateurs ensemble
--> BC=QRC/2PQ --> B=R/2P
-
Malamat
- Membre Relatif
- Messages: 107
- Enregistré le: 03 Oct 2009, 13:36
-
 par Malamat » 17 Oct 2009, 07:54
par Malamat » 17 Oct 2009, 07:54
Effectivement je n'arrivais pas à supprimer le

au dénominateur. Merci encore Ericovitchi :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités