Exercice Polynôme

[scorpioneser]

Bonjour à tous et merci d'avance à ceux prendront le temps de répondre alors voilà j'ai un exercice sur les polynômes :

f(x)= x^4-4x²+3

Montrer que -1 est une racine de f donc bon facile on remplace :

f(-1) = (-1)^4-4(-1)²+3
=1-4+3 = 0 là on est content

Ensuite montrer que pour tout x appartient à R f(x) = ( x-1)g(x) ou g est un polynôme que l'on precisera donc me semble que j'applique mon théorème :

Comme -1 est une racine de f(x) il existe un second polynôme de degré n-1 donc de degré 3 .

J'ai donc : ( x-1) ( ax^3+bx+c) pour préciser (x-1) [(-1)^3+4(-1)+3]

Ensuite il me demande de montrer que ;)3 est une racine de g(x) sauf que quand je remplace :

[(;)3)^3+4(;)3)-3] j'obtient pas 0 je me demande donc si l'erreur vient pas de ma formule plus haut pour g(x) . Possible de m'éclairer à ce sujet ?

[Tenchoun]

Hum, pas sur que ça t'aide beaucoup, mais tu as une équation bicarrée.
Si tu remplaces x^2 par X, tu auras un polynome du degré deux, et il ne te suffira plus qu'à trouver toutes les racines possibles ;)

[scorpioneser]

Euh ou sa ? o_O

[annick]

Bonjour,
tu as mis que g(x) est de la forme ( ax^3+bx+c), mais ne crois-tu pas que c'est plutôt ax^3+bx²+cx+d ?

[scorpioneser]

Ben je me trompe sûrment mais pour moi degré n-1 s'applique partout donc comme on a :

x^4-4x²+3 sa donnerai ( dans mon idée ) x^3-4x+3 on enlève un degré partout non ?

[Ericovitchi]

Et non le n-1 ne s'applique pas partout. Ca c'est une règle que tu as inventée. Suis le conseil d'annick

[scorpioneser]

En effet , j'ai bien dû inventer cette règle -_-' même dans mon cour elle y est plus pourtant j'étais certain qu'elle y était ( conspiration sans aucun doute )

[mathelot]

de toutes façons, ton équation est bicarrée comme l'a souligné Tenchoun:

ça signifie que le polynome de degré 4 est un trinôme du second degré
par rapport à la quantité

il suffit donc de poser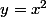
et de factoriser le trinome de la variable y.

[mathelot]

une autre façon de voir est d'écrire que
est le début de

[scorpioneser]

Hum j'ai du mal à suivre déjà pour préciser g :
f(x)= (x+1)(ax^3+bx²+c)
=(x+1)(-1^3+4(-1)²+3
=(x+1)(-3+4+3)
C'est sa ?

[mathelot]

Hum j'ai du mal à suivre déjà pour préciser g :
f(x)= (x+1)(ax^3+bx²+c)
=(x+1)(-1^3+4(-1)²+3
=(x+1)(-3+4+3)
C'est sa ?

non. relis le post #2 :marteau:

[scorpioneser]

Je pourrai avoir un exemple je comprend rien du tout :/

[mathelot]

f(x)= x^4-4x²+3

je t'explique "bicarrée"

(1)

ça vient des exposants

dans l'égalité (1), f(x) est fonction de x par l'intermédiaire de

je remplace formellement (formellement=sans comprendre)
par y.



on obtient une nouvelle fonction,notée g, de la variable

ça va ?

[scorpioneser]

Il a expliquer le cours aujourd'hui en classe la dessus je te remercie pour cette explication supplémentaire :)

[mathelot]

re,

ta factorisation avec du degré 3 donne l'idée d'une "réciproque":

à quelles conditions un quadrinôme (excusez pour ce néologisme
désignant un polynôme de degré 3)
est facteur dans la factorisation d'un polynome bicarré (de degré 4).