D.m.

[megh]

bonjour je bute sur la dernière partie d'un exercice:

dans un repère orthonormé, on place A(-3;-1) ;B(11;1);C(6;5) D(-1;4)

5) si M appartient à (AC), quelle équation reliant x et y doit etre vérifiée?

6)en deduire une equation de la droite (AC) e la forme y=ax+b

merci de me repondre (pour la 5 je sais que les vecteurs AM et AC sont colineaires)

[darkanett]

voilà, pour la 5 tu as deviné, pour la 6, je te conseille de résoudre un système d'équations pour trouver a et b dans y=ax+b
-1=-3a+b
5= 6a+b
et là tu obtiens tes a et B pour l'équation

[megh]

MERCI

mais je sais pour la 5 que les vecteurs AM et AC sont colineaires mais comment rediger? pour :'' quelle equation reliant x et y doit etre verifiée,""

[megh]

MERCI

mais je sais pour la 5 que les vecteurs AM et AC sont colineaires mais comment rediger? pour :'' quelle equation reliant x et y doit etre verifiée,""

[megh]

bonjour

en prenant les coordonnées qui sont proportionnelles des vecteurs AM et AC colineaires j'ai trouvé:
y=2/3x-3 (equation de la droite AC
es ce juste ? merci

[mathelot]

bonjour,

trois méthodes

1° méthode
partir de y=ax+b
remplacer (x,y) par et
on obtient un système 2x2 d'inconnues a et b
2° méthode
écrire les coordonnées des vecteurs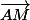 et
où M est le point générique de (AC)
annuler det()

3° méthode
écrire que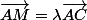 (2 coordonnées=2 égalités)
où est l'abscisse de M dans le repère
éliminer entre les deux égalités en le calculant de deux manières différentes et en égalisant les résultats.