Soit
J'ai trouvé la relation suivante ( qui était demandé dans l'énoncé ) :
( je ne sais pas d'ou vient la fleche ne faites pas attention )
Je dois démontrer que lorsque
Merci
Integrale impropre
2 messages
- Page 1 sur 1
Integrale impropre
par amk » 25 Fév 2006, 21:51
Bonsoir ,
Soit
=\int_{2}^{+\infty}\frac{\cos \left (2\cdot \pi \cdot y \cdot x \right)}{x \cdot \ln(x) } dx)
J'ai trouvé la relation suivante ( qui était demandé dans l'énoncé ) :
 = \int_{2}^{1/y}\frac{\cos \left (2\cdot \pi \cdot y \cdot x \right)-1}{x \cdot \ln(x) } dx + \int_{2}^{1/y}\frac{dx}{x \cdot \ln x } + \int_{1/y}^{+\infty}\frac{ cos \left (2\cdot\pi \cdot y \cdot x \right)}{x \cdot \ln x })
( je ne sais pas d'ou vient la fleche ne faites pas attention )
Je dois démontrer que lorsque
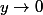
on a  \simeq \ln \left(-\ln y \right))
Merci
Soit
J'ai trouvé la relation suivante ( qui était demandé dans l'énoncé ) :
( je ne sais pas d'ou vient la fleche ne faites pas attention )
Je dois démontrer que lorsque
Merci
par Pythales » 26 Fév 2006, 18:19
En posant 
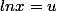
on vérifie que l'intégrale du milieu est effectivement équivalente à ))
lorsque y tend vers zéro. Il reste à montrer que les intégrales 1 et 3 gardent une valeur finie, ou du moins tendent vers l'infini "moins vite" que la 2. Facile pour la 1, moins évident pour la 3, avec la borne 
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :