Produit vectoriel

par **Khaize** » 11 Oct 2009, 10:23

Bonjour à tous, voila j'ai un exercice à faire et je bloque complètement alors que c'est peut être tous simple :

Soit un repère orthonormal (O, i ,j ,k ) et u un vecteur unitaire

1) Calculer ||u^i||² + ||u^j||² + ||u^k||²
Pour ceci j'ai trouvé un résultat mais il ne m'avance pas trop:
||u^i||² + ||u^j||² + ||u^k||² = sin²(u;i) + sin²(u;j) + sin²(u;k) car ||u|| = ||i||=||j|| = ||k|| = 1

2) Montrer que l'un des trois nombres ||u^i|| ; ||u^j|| ;||u^k|| est supérieur ou égal a racine(2/3)
Et là je n'est aucune idée.
Voila merci d'avance pour votre aide.

par **AlexisD** » 11 Oct 2009, 10:41

Je pense qu'il peut être utile de travailler en coordonnées sphériques, si tu en as déjà entendu parler.
Comme le vecteur u est unitaire, ca devrait simplifier la tâche...

par **yos** » 11 Oct 2009, 11:06

Tu as des carrés en trop sur tes sinus.

En prenant u(x,y,z), ça va bien aussi : ta somme vaut

.
Ensuite si ces trois termes sont <2/3, la somme de leur carré est <4/3, ce qui est absurde car elle vaut 2.

par **Khaize** » 11 Oct 2009, 11:16

Merci pour vos réponses mais j'avais oublié de mettre les norme au carré. Est-ce que l'usage des coordonnées sphériques est toujours possibles?

par **Khaize** » 11 Oct 2009, 11:33

A vrai dire je viens juste de voir les coordonnées sphériques pour un point, donc pour un produit vectoriel, faut-il que je le calcule en coordonnées carthésienne et ensuite que je l'exprime en coordonnées sphériques?

par **AlexisD** » 11 Oct 2009, 11:37

Tu peux toujours écrire ton vecteur u:

On vérifie que u est effectivement unitaire, le calcul du produit vectoriel est simple ainsi que la somme des carrés des normes qui vaut effectivement 2.

Pour la deuxième question, je n'ai rien à ajouter, on t'a déjà répondu.

par **Khaize** » 11 Oct 2009, 11:41

D'accord merci beaucoup pour ta réponse, je vais essayer de calculer sa alors ^^

par **Khaize** » 11 Oct 2009, 11:59

Voila, après calculs, j'obtiens:

u^i (0;sin(téta);-cos(téta)sin(phi))
u^j (-sin(téta);0;cos(téta)cos(phi))
u^k (cos(téta)sin(phi);-cos(téta)cos(phi);0)

donc j'obtiens:||u^i||² + ||u^j||² + ||u^k||² = 2sin²(téta) + 2cos²(téta)cos²(phi) + 2cos²(téta)sin²(phi)

Comment montrer alors que sa vaut 2?

par **AlexisD** » 11 Oct 2009, 12:22

Utilise le fait que

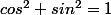
grâce à une première factorisation.

par **Khaize** » 11 Oct 2009, 12:23

exercice résolu

par **Khaize** » 11 Oct 2009, 12:23

merci ^^ je venais juste de trouvé ^^ merci encore

Produit vectoriel

produit vectoriel

Qui est en ligne