Amusant
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 24 Fév 2006, 17:25
par Pythales » 24 Fév 2006, 17:25
Montrer que :
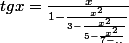
-
leibniz
- Membre Relatif
- Messages: 407
- Enregistré le: 30 Mai 2005, 10:00
-
 par leibniz » 24 Fév 2006, 17:28
par leibniz » 24 Fév 2006, 17:28
Bonjour;
C'est quoi ça pythales? même pas un bonjour...
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 24 Fév 2006, 22:15
par quinto » 24 Fév 2006, 22:15
Pythales a écrit:Montrer que :
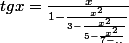
C'est trivial

Il suffit de faire un développement en série. C'est un résultat du à Euler.
J'ai justement fait un séminaire sur le sujet en Décembre, si je retrouve le document, je peux le faire parraitre sur le site

(et si ca en intéresse)
A+
-
hassan_smia
- Membre Naturel
- Messages: 12
- Enregistré le: 05 Nov 2005, 18:40
-
 par hassan_smia » 25 Fév 2006, 10:33
par hassan_smia » 25 Fév 2006, 10:33
slt ....
ça m'interresse aussii.. est se c'est un developemnt de mc laurent ou qoi?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 25 Fév 2006, 10:58
par Pythales » 25 Fév 2006, 10:58
Bon, alors bonjour quand même (Leibniz a raison).
Cela dit, ça ne me parait pas si trivial que ça. Le "il suffit" me semble un peu prématuré ...
-
Anonyme
 par Anonyme » 25 Fév 2006, 11:15
par Anonyme » 25 Fév 2006, 11:15
quinto a écrit:C'est trivial

Il suffit de faire un développement en série. C'est un résultat du à Euler.
J'ai justement fait un séminaire sur le sujet en Décembre, si je retrouve le document, je peux le faire parraitre sur le site

(et si ca en intéresse)
A+
Mmmm .... Pourquoi faire un séminaire sur un sujet trivial ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 25 Fév 2006, 11:22
par Pythales » 25 Fév 2006, 11:22
Un début ?
^n\frac{x^{2n+1}}{(2n+1)!}}{\sum(-1)^n\frac{x^{2n}}{(2n!)}})
^n\frac{x^{2n}}{(2n)!}}{\sum(-1)^n\frac{x^{2n}}{(2n+1)!}})
et essayer de mettre le rapport

sous la forme 1-U d'où U=...
C'est aussi pénible à calculer que de rédiger en latex.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
(et si ca en intéresse)
