Montrer qu'une fonction est C1

[bertrand_8956]

bonjour

j'ai a montre qu'une fonction est C1([0,1],R)
cette fonction est
g(x)=ln(x)*integrale(0,x)de(f(t)dt)+integrale(x,1)de(ln(t)*f(t)dt) pour x>0
g(0)=I quelconque a priori

f est une fonction continue de [0,1] dans R

le probleme pour moi est de montrer la definition et la continuité de la derivee en 0

merci de vos reponses

[redwolf]

Traduction :

pour

.

[redwolf]

Bonjour.

ne peut pas être quelconque, puisqu'il faut que soit continue. Il faut donc d'abord prouver que admet une limite en 0. En dérivant (pour 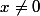), on trouve

où est une primitive de sur . Comme , on peut écrire :



La fonction sous le signe est continue sur sa valeur en 0 est .

admet donc une limite en 0, et on pose .

Enfin, , ce qui suffit à prouver que est dérivable en 0, de dérivée , et que est continue en 0.