Bonjour à tous
voila je suis en master 1 science du management
j'ai un exercice en math fi et j'aimerai savoir si mon raisonnement est correcte.
voici l'énonce:
une entreprise fait des versement chaque année pendant 15 ans de valeur constante pour financier un voyage dont le cout actuelle est de 3 000 000 euro
- les 5 première année le taux est de 5%
- les 5 autre le taux est de 7%
- et les 5 dernier le taux est 9%
on cherche les versement ?
j'ai utilise cet formule Vn=a*(((((1+i)^-n)-1)/i)
ce qui me donne : 3000 000 = x*((((1+0.05)^-5)-1)/0.05)+(1+0.07)^-5)-1)/0.07)+(1+0.09)^-5)-1)/0.09)
ce qui donne une annuité constant de 243 519.83 euro
est-ce-que vous pourriez me dire si c'est correcte?
cordialement
Math financiére
7 messages
- Page 1 sur 1
tournels83 a écrit:j'ai utilise cet formule Vn=a*(((((1+i)^-n)-1)/i)
ce qui me donne : 3000 000 = x*((((1+0.05)^-5)-1)/0.05)+(1+0.07)^-5)-1)/0.07)+(1+0.09)^-5)-1)/0.09)
bonsoir,
je ne sais pas. pour obtenir la valeur actuelle,
j'aurai actualisé les flux à 7% sur une période plus longue que 5 ans,
pour tenir compte de la pré-période calendaire de cinq ans qui a précédé.
Parce que les flux au taux de 7% sont situés sur le calendrier des dates
de valeurs après une 1ère période de cinq années.
Ton calcul n'est surement pas correct.
Pour 15 annuités à 243 000 , ça fait plus de 3 600 000 de versement.
Pour toucher au final 3 000 000 , c'est dommage!
Mieux vaut mettre l'argent sous le matelas...
Change de banquier tout de suite s'il te fait une proposition pareille!
Sinon pour ton problème, est-ce qu'il s'agit d'intérêts simples ou composés?
S'ils sont simples
c'est 3000000 = x * (15 + 0.05*15 + 0.07*30 + 0.09*45)
S'ils sont composés
3000000 = x * (
((1.05)^5-1)*(1.05)/0.05*(1.07)^5*(1.09)^5
+
((1.07)^5-1)*(1.07)/0.07*(1.09)^5
+
((1.09)^5-1)*(1.09)/0.09)
Si je n'ai pas fait d'erreur de calcul ça devrait faire
139986 dans un cas
105220 dans l'autre
Pour 15 annuités à 243 000 , ça fait plus de 3 600 000 de versement.
Pour toucher au final 3 000 000 , c'est dommage!
Mieux vaut mettre l'argent sous le matelas...
Change de banquier tout de suite s'il te fait une proposition pareille!
Sinon pour ton problème, est-ce qu'il s'agit d'intérêts simples ou composés?
S'ils sont simples
c'est 3000000 = x * (15 + 0.05*15 + 0.07*30 + 0.09*45)
S'ils sont composés
3000000 = x * (
((1.05)^5-1)*(1.05)/0.05*(1.07)^5*(1.09)^5
+
((1.07)^5-1)*(1.07)/0.07*(1.09)^5
+
((1.09)^5-1)*(1.09)/0.09)
Si je n'ai pas fait d'erreur de calcul ça devrait faire
139986 dans un cas
105220 dans l'autre
Bonjour
Mes calculs ne correspondent pas avec ceux des autres membres, du moins je le pense car déjà, je n'arrive pas à bien lire les formules lol. Je te propose ma solution: il s'agit d'un problème de macroéconomie simple sur le taux d'intérêt actualisé:
}+\frac{x}{(1+0,05)^2}+\frac{x}{(1+0,05)^3}+\frac{x}{(1+0,05)^4}+\frac{x}{(1+0,05)^5}+<br />+\frac{x}{(1+0,05)^5(1+0,07)}+\frac{x}{(1+0,05)^5(1+0,07)^2}+\frac{x}{(1+0,05)^5(1+0,07)^3}+\frac{x}{(1+0,05)^5(1+0,07)^4}+\frac{x}{(1+0,05)^5(1+0,07)^5}+\frac{x}{(1+0,05)^5(1+0,07)^5(1+0,09)}+\frac{x}{(1+0,05)^5(1+0,07)^5(1+0,09)^2}+\frac{x}{(1+0,05)^5(1+0,07)^5(1+0,09)^3}+\frac{x}{(1+0,05)^5(1+0,07)^5(1+0,09)^4}+\frac{x}{(1+0,05)^5(1+0,07)^5(1+0,09)^5})
Comme nous pouvons voir ici, plus on s'éloigne dans le temps plus la valeur actuelle du versement futur est petite (à un moment donné la formule bugue mais le principe est le même)
}+\frac{x}{(1,05)^2}+\frac{x}{(1,05)^3}+\frac{x}{(1,05)^4}+\frac{x}{(1,05)^5}++\frac{x}{(1,05)^5(1,07)}+\frac{x}{(1,05)^5(1,07)^2}+\frac{x}{(1,05)^5(1,07)^3}+\frac{x}{(1,05)^5(1,07)^4}+\frac{x}{(1,05)^5(1,07)^5}+\frac{x}{(1+0,05)^5(1+0,07)^5(1,09)}+\frac{x}{(1+0,05)^5(1+0,07)^5(1,09)^2}+\frac{x}{(1+0,05)^5(1+0,07)^5(1,09)^3}+\frac{x}{(1+0,05)^5(1+0,07)^5(1,09)^4}+\frac{x}{(1+0,05)^5(1+0,07)^5(1,09)^5})
}+\frac{1}{(1,05)^2}+\frac{1}{(1,05)^3}+\frac{1}{(1,05)^4}+\frac{1}{(1,05)^5}++\frac{1}{(1,05)^5(1,07)}+\frac{1}{(1,05)^5(1,07)^2}+\frac{1}{(1,05)^5(1,07)^3}+\frac{1}{(1,05)^5(1,07)^4}+\frac{1}{(1,05)^5(1,07)^5}+\frac{1}{(1+0,05)^5(1+0,07)^5(1,09)}+\frac{1}{(1+0,05)^5(1+0,07)^5(1,09)^2}+\frac{1}{(1+0,05)^5(1+0,07)^5(1,09)^3}+\frac{1}{(1+0,05)^5(1+0,07)^5(1,09)^4}+\frac{1}{(1+0,05)^5(1+0,07)^5(1,09)^5}))
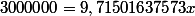
x=308800,302951
15x=4 632 004,544265
La valeur est supérieure à 3 000 000 de départ c'est normal car c'est le cout du crédit à 15 ans pour financer le voyage d'aujourd'hui, avec les taux particulièrement élevés qui sont de 5 7 et 9%. Si l'on regarde le taux d'inflation en même temps, cette valeur se verra réduite...
Cordialement
Mes calculs ne correspondent pas avec ceux des autres membres, du moins je le pense car déjà, je n'arrive pas à bien lire les formules lol. Je te propose ma solution: il s'agit d'un problème de macroéconomie simple sur le taux d'intérêt actualisé:
Comme nous pouvons voir ici, plus on s'éloigne dans le temps plus la valeur actuelle du versement futur est petite (à un moment donné la formule bugue mais le principe est le même)
x=308800,302951
15x=4 632 004,544265
La valeur est supérieure à 3 000 000 de départ c'est normal car c'est le cout du crédit à 15 ans pour financer le voyage d'aujourd'hui, avec les taux particulièrement élevés qui sont de 5 7 et 9%. Si l'on regarde le taux d'inflation en même temps, cette valeur se verra réduite...
Cordialement
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
