Devoir Maison: Fonctions variations et extremum
18 messages
- Page 1 sur 1
Devoir Maison: Fonctions variations et extremum
Bonjour !
Après avoir réussi (au bout de quelques heures de réflexions) mon exercice sur les barycentres, je bloque sur mon devoir maison (dur, dur la première s).
Je vous montre le premier exercice ?
EXERCICE 1 : On se propose d'étudier les variations de la fonctions Cube.
1) Vérifier l'égalité a^3 - b^3 = ( a - b )( a^2 + ab + b^2 )
Déjà, si je résolvais cette question, ça m'aiderais.
J'ai déjà essayé, mais le problème, c'est que je n'y arrive pas.
J'ai fait quelques calculs, mais rien de bien convaincant...
Ca m'aurait arrangé si ça avait été ( a^2 + 2ab + b^2 ) pour faire une identité remarquable, mais non !!
Quelqu'un peut m'aider ? Merci beaucoup d'avance.
Après avoir réussi (au bout de quelques heures de réflexions) mon exercice sur les barycentres, je bloque sur mon devoir maison (dur, dur la première s).
Je vous montre le premier exercice ?
EXERCICE 1 : On se propose d'étudier les variations de la fonctions Cube.
1) Vérifier l'égalité a^3 - b^3 = ( a - b )( a^2 + ab + b^2 )
Déjà, si je résolvais cette question, ça m'aiderais.
J'ai déjà essayé, mais le problème, c'est que je n'y arrive pas.
J'ai fait quelques calculs, mais rien de bien convaincant...
Ca m'aurait arrangé si ça avait été ( a^2 + 2ab + b^2 ) pour faire une identité remarquable, mais non !!
Quelqu'un peut m'aider ? Merci beaucoup d'avance.
C'est vrai, je ne suis pas très intelligente !
alors ( a - b )( a² + ab + b² ) = ( a^3 - b^3 ).
Merci beaucoup !
La deuxième question, c'est:
2) Soit a et b 2 Réels positifs tels que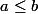
a) Etudier le signe de l'expression a²+ab+b²
b) A l'aide de l'égalité précédente en déduire le signe de la différence a^3 - b^3.
c) Donner alors le sens de variation de la fonction cube sur [0; +infini[
_________
Mes réponses :
a)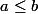
 (car la fonction carrée est croissante pour les nombres positifs)
(car la fonction carrée est croissante pour les nombres positifs)

Après, je ne sais pas...
alors ( a - b )( a² + ab + b² ) = ( a^3 - b^3 ).
Merci beaucoup !
La deuxième question, c'est:
2) Soit a et b 2 Réels positifs tels que
a) Etudier le signe de l'expression a²+ab+b²
b) A l'aide de l'égalité précédente en déduire le signe de la différence a^3 - b^3.
c) Donner alors le sens de variation de la fonction cube sur [0; +infini[
_________
Mes réponses :
a)
Après, je ne sais pas...
Nyfa a écrit:Mais je suis bête !
On sait que a et b sont positifs, donc a² est positif, ab est positif et b² est positif...
Donc a²+ab+b² est positif !
b) signe de la différence?
Je sais que= ( a - b )( a² + ab + b² )
Or ( a² + ab + b² ) est positif
Et ( a - b ) est négatif car
Doncest négatif !
C'est ça ?
oui exactement, on a répondu en même temps
Donc j'ai trouvé, merci !
c)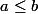
 donc
donc 
Les images sont rangées dans le même sens que les antécédents donc la fonctions cube est croissante sur [0;+infini[ !
3) Reprendre le raisonnement précédent avec a et b deux réels négatifs.
En déduire les variations de la fonction cube sur ]-infini;0]
4) Dresser le tableau de variation de la fonctions cube sur R.
-> Tout ça devient facile a présent, je devrais m'en sortir. Merci beaucoup, en tout cas !
A présent, le deuxième et dernier exercice (qui me pose problème aussi) !
EXERCICE 2
Voici l'énoncé :
http://www.hostingpics.net/viewer.php?id=510141numerisation0001.jpg
Je pourrais avoir une piste, pour commencer, s'il vous plait ?
c)
Les images sont rangées dans le même sens que les antécédents donc la fonctions cube est croissante sur [0;+infini[ !
3) Reprendre le raisonnement précédent avec a et b deux réels négatifs.
En déduire les variations de la fonction cube sur ]-infini;0]
4) Dresser le tableau de variation de la fonctions cube sur R.
-> Tout ça devient facile a présent, je devrais m'en sortir. Merci beaucoup, en tout cas !
A présent, le deuxième et dernier exercice (qui me pose problème aussi) !
EXERCICE 2
Voici l'énoncé :
http://www.hostingpics.net/viewer.php?id=510141numerisation0001.jpg
Je pourrais avoir une piste, pour commencer, s'il vous plait ?
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
