Exo congruences et Fermat

par **maxou22** » 09 Oct 2009, 09:00

Bonjour,
Je suis sur un exercice qui me résiste même si j'ai l'impression que je ne suis pas loin.
Enoncé:
n premier impair
Montrer que si un nombre premier p divise 2^(n)-1 alors 2n divise p-1.

Ma démarche:
p divise 2^(n)-1 donc il existe q dans Z / pq=2^(n)-1

n premier et pgcd(2,n)=1 car n est impair
donc j'applique Fermat: n divise 2^(n-1)-1 => 2n divise 2^(n)-1-1
=>2n divise pq-1

mais je n'arrive pas a montrer que p-1 est congru à 0 mod[2n]

Je suis là et je surveille le topic donc si vous voulez bien m'aider je peux répondre rapidement.
Merci d'avance pour vos idées

par **yos** » 09 Oct 2009, 10:16

p divise

(hyp.) ainsi que

(Fermat), donc il divise leur PGCD qui est

.

par **maxou22** » 09 Oct 2009, 12:02

D'accord il fallait remarquer la dernière égalité ^_^. Bon je planche sur sa démo. Merci pour l'explication Yos.

par **busard_des_roseaux** » 09 Oct 2009, 16:07

yos a écrit:p divise (hyp.) ainsi que (Fermat), donc il divise leur PGCD qui est .

Bonsoir Yos,

comment est-ce que tu conclues ?

par **skilveg** » 09 Oct 2009, 16:34

Bonsoir,

Personnellement, je considérerais l'ordre de

dans

(ce qui donne puisque

est premier

) et le fait que

et

soient impairs.

par **yos** » 09 Oct 2009, 16:39

busard_des_roseaux a écrit:comment est-ce que tu conclues ?

Salut.
eh ben le pgcd en exposant vaut 1 ou n car n est premier.
1 c'est exclu (comme

est multiple de p).
Donc ce pgcd est n, donc n divise p-1.
Par ailleurs 2|p-1 et 2 est premier à n donc 2n divise p-1.

par **mathelot** » 09 Oct 2009, 18:18

yos a écrit:eh ben le pgcd en exposant est multiple de p

je te prie de m'excuser. je ne vois pas :hum:

par **yos** » 09 Oct 2009, 18:27

Non, j'ai écrit trop vite; c'est l'autre pgcd qui est multiple de p :

Donc PGCD(n,p-1) peut pas valoir 1.
J'ai corrigé mon message précédent.

par **maxou22** » 09 Oct 2009, 18:45

Ok pour la conclusion.
Par contre pour le fait que pgcd(2^(n)-1, 2^(p-1)-1)=2^(pgcd(n,p-1))-1 , je trouve pas.
J'ai bien la division de droite à gauche (en passant par les series géometriques) mais dans l'autre sens...non
Je continue quand même.

Et aussi, j'aimerais bien savoir comment on fait pour écrire les expressions aussi joliment.

par **yos** » 09 Oct 2009, 19:03

De façon générale,

.
avec

pour PGCD.
On peut même faire encore plus général :

.

Suppose n>m. Si d divise le premier membre, il divise aussi

, c'est-à-dire

et tu peux descendre ainsi jusqu'à avoir le PGCD en exposant (algorithme d'Euclide).

par **yos** » 10 Oct 2009, 06:36

L'ensemble est donc assez contorsionné, et tout ça pour pas faire de théorie des groupes (cf message de skilveg).
On peut donner une autre preuve (pas vraiment différente, mais peut-être plus claire), qui colle un peu plus à la preuve algébrique :

On note E l'ensemble des entiers k>0 tels que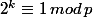

. Cet ensemble possède un plus petit élément e et une division euclidienne montre que

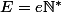. Cet ensemble E contient n et p-1 et il est alors clair que e=n et donc que n|p-1.

par **maxou22** » 10 Oct 2009, 10:12

Contorsionné peut être mais instructif. Cela dit ta première demonstration fonctionne que si on sait que p-1 > n sinon 2n ne divise pas p-1

par **yos** » 10 Oct 2009, 10:26

p-1>n est une conséquence de la démonstration (je l'utilise pas il me semble).

par **maxou22** » 10 Oct 2009, 11:40

Oui c'est vrai que c'est que c'est pas nécessaire. :++:

par **yos** » 10 Oct 2009, 13:18

Cet exercice permet de montrer qu'un diviseur premier d'un nombre de Mersenne

(

, n premier > 2) est nécessairement de la forme 2kn+1.

par **maxou22** » 10 Oct 2009, 15:18

Heu ok c'est bon à savoir.
Je crois que je vais faire un petit tour sur wikipedia parce que quelque chose me dit que ca me sera bientôt utile.

Exo congruences et Fermat

Exo congruences et Fermat

Qui est en ligne