salut,
je veux savoir comment montrer que n'importe quel suite est divergente
c a dire le shemin a suivre pour montrer que la suite est divergente
avec un exemple simple pour mieux comprendre
merci d'avance
Suite convergente
6 messages
- Page 1 sur 1
Il suffit de prendre la négation d'un critère de convergence
Une suite n'a pas de limite finie si
n'a pas de limite finie si
il existe tel que pour tout
tel que pour tout  il existe
il existe 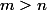
tel que
Une suite ne tend pas vers
ne tend pas vers  si
si
il existe tel que pour tout
tel que pour tout  il existe
il existe 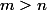
tel que
Mais bon je ne vois quel exemple t'éclairerait plus.
Essaie de te faire la main avec
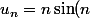)
Une suite
il existe
tel que
Une suite
il existe
tel que
Mais bon je ne vois quel exemple t'éclairerait plus.
Essaie de te faire la main avec
tu peux aussi minorer ta suite par une suite divergente connue, exemple très simple : Un= n²
Tu connais par exemple la suite de référence Vn=n, qui diverge bien sur
tu pourrais dire Un > Vn et Vn diverge, donc Un diverge
(bon ici tu peux dire directement que Un diverge, mais c'est pour illustrer...)
ou encore calculer Un+1/Un et voir que le quotient ne tend pas vers 0 en +oo, etc...
Tu connais par exemple la suite de référence Vn=n, qui diverge bien sur
tu pourrais dire Un > Vn et Vn diverge, donc Un diverge
(bon ici tu peux dire directement que Un diverge, mais c'est pour illustrer...)
ou encore calculer Un+1/Un et voir que le quotient ne tend pas vers 0 en +oo, etc...
Deux solutions : soit la suite n'est pas bornée et tu trouves une sous-suite qui tend vers l'infini.
Soit la suite est bornée (c'est ton cas) et tu dois trouver deux sous suites ayant des limites distinctes.
Si ta suite est un=cos(n*pi), tu peux regarder la sous suite vn=u2n et wn=u(2n+1)...
Si c'est de la forme n*p ou p est un entier c'est plus compliqué (car il y a une infinité de valeurs d'adhérence) mais il doit sans doute être possible de construire une suite positive minorée et une négative majorée de telle sorte que le définition de limite ne peut être vérifiée.
Soit la suite est bornée (c'est ton cas) et tu dois trouver deux sous suites ayant des limites distinctes.
Si ta suite est un=cos(n*pi), tu peux regarder la sous suite vn=u2n et wn=u(2n+1)...
Si c'est de la forme n*p ou p est un entier c'est plus compliqué (car il y a une infinité de valeurs d'adhérence) mais il doit sans doute être possible de construire une suite positive minorée et une négative majorée de telle sorte que le définition de limite ne peut être vérifiée.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
