Sommes + limites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 08 Oct 2009, 11:45
par doodilight » 08 Oct 2009, 11:45
bonjour ^^
voilà, je suis en L3 de mathématique, et j'ai un DM à faire...
voilà une parti des questions que j'ai :
-calculer la somme :
 (a^n/n!)})
-limite en l'infini de l'intégrale :
\sin(nx))/x^{1/2}}dx)
-limite en l'infini de l'intégrale :
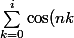/(1+nk^{2})})
(i = infini pour le dernier ^^)
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 08 Oct 2009, 12:36
par wserdx » 08 Oct 2009, 12:36
C'est dommage, parce que ce n'est pas lisible.
Essaie quelquechose comme
\sum_{k=0}^n{k \exp(a) a^n/n!}
puis mets les balises TEX, ca donne ça:
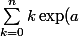 a^n/n!})
Pareil pour
\int_0^\infty{\exp(-nx)\sin(nx)/x^{1/2}}dx
\sin(nx)/x^{1/2}}dx)
ca aidera grandement à la compréhension.
Il y plein de sites pour apprendre "Latex".
C'est très utile pour les matheux, mais pas seulement...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 08 Oct 2009, 12:53
par Nightmare » 08 Oct 2009, 12:53
Salut !
Quel est le cours sur lequel est basé ce DM (voir les outils qu'on peut utiliser)
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 08 Oct 2009, 12:54
par doodilight » 08 Oct 2009, 12:54
Nightmare a écrit:Salut !
Quel est le cours sur lequel est basé ce DM (voir les outils qu'on peut utiliser)
c'est un cours d'intégration!!!
mesure de Lebesgue, tribu, mesure, fonction borelienne etc...
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 08 Oct 2009, 12:57
par doodilight » 08 Oct 2009, 12:57
wserdx a écrit:C'est dommage, parce que ce n'est pas lisible.
Essaie quelquechose comme
\sum_{k=0}^n{k \exp(a) a^n/n!}
puis mets les balises TEX, ca donne ça:
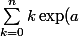 a^n/n!})
Pareil pour
\int_0^\infty{\exp(-nx)\sin(nx)/x^{1/2}}dx
\sin(nx)/x^{1/2}}dx)
ca aidera grandement à la compréhension.
Il y plein de sites pour apprendre "Latex".
C'est très utile pour les matheux, mais pas seulement...
merci beaucoup!!!
en effet, c'est plus lisible ^^
je suis désolé mais je ne suis pas habitué au forum!
enfin bref merci ^^
-
Pauline03081994
- Membre Naturel
- Messages: 17
- Enregistré le: 09 Avr 2009, 16:52
-
 par Pauline03081994 » 08 Oct 2009, 13:02
par Pauline03081994 » 08 Oct 2009, 13:02
Pouvez vous m'aidez a faire notre dm, car je vois que vous etes très intelligent --' rubrique lycée premiere rubrique.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 08 Oct 2009, 18:46
par Pythales » 08 Oct 2009, 18:46
Pour la 2 tu peux essayer
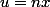

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 08 Oct 2009, 19:03
par nuage » 08 Oct 2009, 19:03
Salut,
la première somme est triviale :
}2)
et le fait que

soit multiplié par quelque chose de constant n'y change rien.
Es tu certain de l'énoncé ?
-
mathelot
 par mathelot » 08 Oct 2009, 19:10
par mathelot » 08 Oct 2009, 19:10
nuage a écrit:Salut,
la première somme est triviale :
}2)
et le fait que

soit multiplié par quelque chose de constant n'y change rien.
Es tu certain de l'énoncé ?
c probablement

-
mathelot
 par mathelot » 08 Oct 2009, 19:17
par mathelot » 08 Oct 2009, 19:17
doodilight a écrit:-limite en l'infini de l'intégrale :
\sin(nx))/x^{1/2}}dx)
pour celle-çi, l'intégrande est un produit de 3 fonctions.
comment vas-tu les grouper astucieusement ?
est-ce une véritable singularité en x=0 ?
s'il n'y a pas de singularité , c'est que ...
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 09 Oct 2009, 07:37
par doodilight » 09 Oct 2009, 07:37
mathelot a écrit:c probablement

oui c'est 'a' puissance 'k'
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 09 Oct 2009, 12:46
par doodilight » 09 Oct 2009, 12:46
mathelot a écrit:pour celle-çi, l'intégrande est un produit de 3 fonctions.
comment vas-tu les grouper astucieusement ?
est-ce une véritable singularité en x=0 ?
s'il n'y a pas de singularité , c'est que ...
c'est que?!
sinon tout ce qui a été dit jusque la j'y ai deja pensé mais ca ne m'avance pas beaucoup, en fait... Y a-t-il quelqu'un qui puisse me sortir la tête de l'eau... j'ai tjrs hait les intégrales, les limites et les sommes... je suis servies ^^
-
mathelot
 par mathelot » 09 Oct 2009, 14:38
par mathelot » 09 Oct 2009, 14:38
doodilight a écrit:c'est que?!
j'ai tjrs hait les intégrales, les limites et les sommes... je suis servies ^^
sinon, tu peux étudier Platon ou Kierkegaard :we:
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 09 Oct 2009, 14:45
par doodilight » 09 Oct 2009, 14:45
mathelot a écrit:sinon, tu peux étudier Platon ou Kierkegaard :we:
mouai, euh nan... je vais rester avec mes intégrales ^^...
Et puis, je vais pas baisser les bras, un jour je comprendrais, ptetre même que je trouverais ça "trivial" lol
-
mathelot
 par mathelot » 09 Oct 2009, 14:46
par mathelot » 09 Oct 2009, 14:46
doodilight a écrit:-limite en l'infini de l'intégrale :
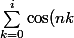/(1+nk^{2})})
(i = infini pour le dernier ^^)
pour la (3), tu peux pas essayer un théorème de convergence dominée
avec des mesures de comptages (discrètes)
)
la série étant dominée par
)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Oct 2009, 15:00
par Pythales » 09 Oct 2009, 15:00
Pour la 2, pourquoi ne pas poser

?
Ca donne

, facile à étudier
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 09 Oct 2009, 15:02
par doodilight » 09 Oct 2009, 15:02
Pythales a écrit:Pour la 2, pourquoi ne pas poser

?
Ca donne

, facile à étudier
Yep on m'avait déjà donné l'idée, ca me donne une limite de zero c'est ça?
merciii ^^
-
doodilight
- Membre Naturel
- Messages: 21
- Enregistré le: 04 Mai 2009, 17:13
-
 par doodilight » 09 Oct 2009, 16:21
par doodilight » 09 Oct 2009, 16:21
mathelot a écrit:pour la (3), tu peux pas essayer un théorème de convergence dominée
avec des mesures de comptages (discrètes)
)
la série étant dominée par
)
je ne connaissais pas ce théorème... je l'ai chercher dans mon cours, il n'y est pas... donc j'ai regarder sur wikipedia...
mais je vois pas trop comment remplacer fn par f... enfin bref, je comprend pas vraiment la façon dont on doit utiliser la formule... pouvez vous juste me donner un exemple d'utilisation s'il vous plait, histoire que je sache comment l'utiliser dans mon cas!
merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités