Les débutants y arrivent mieux que les confirmés
Olympiades mathématiques, énigmes et défis
-
As2piK
- Membre Naturel
- Messages: 18
- Enregistré le: 07 Oct 2009, 16:34
-
 par As2piK » 07 Oct 2009, 19:23
par As2piK » 07 Oct 2009, 19:23
Voici un petit problème assez célèbre, que j'ai découvert dans le livre
Les Foumis de Bernard Werber.
[CENTER]
1
11
21
1211
111211
311221[/CENTER]
Les tout jeunes trouveront plus facilement que les vieux de la vieille des maths !
Trouvez la ligne suivante

-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 07 Oct 2009, 20:14
par Timothé Lefebvre » 07 Oct 2009, 20:14
Bonjour,
ce n'est pas du tout une Olympiade ?
La ligne suivante est 13112221.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Oct 2009, 22:13
par ffpower » 07 Oct 2009, 22:13
et puis ya une erreur dans l enoncé.la 5eme ligne c est 111221( et du coup la ligne d apres n est plus bonne non plus )
-
jamys123
- Membre Relatif
- Messages: 367
- Enregistré le: 27 Mar 2007, 12:18
-
 par jamys123 » 08 Oct 2009, 05:46
par jamys123 » 08 Oct 2009, 05:46
yop,
la suite de Conway, c'était mon tout premier message sur ce forum...arghhh...
allez petite question : est-ce qu'un jour on peut voir apparaître le 4 dans cette suite?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 08 Oct 2009, 09:57
par Timothé Lefebvre » 08 Oct 2009, 09:57
Salut,
je parie que non ! On ne pourrait rien avoir au-dessus de 3 même ...
-
jamys123
- Membre Relatif
- Messages: 367
- Enregistré le: 27 Mar 2007, 12:18
-
 par jamys123 » 08 Oct 2009, 10:59
par jamys123 » 08 Oct 2009, 10:59
Timothé Lefebvre a écrit:Salut,
je parie que non ! On ne pourrait rien avoir au-dessus de 3 même ...
et l'explication???
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 08 Oct 2009, 12:12
par Timothé Lefebvre » 08 Oct 2009, 12:12
A première vue je pense à l'absurde, ou la récurrence, ou les deux ...
Si on a un 4, qu'est-ce qu'on a eu avant pour en arriver là ?
-
jamys123
- Membre Relatif
- Messages: 367
- Enregistré le: 27 Mar 2007, 12:18
-
 par jamys123 » 08 Oct 2009, 12:31
par jamys123 » 08 Oct 2009, 12:31
Timothé Lefebvre a écrit:A première vue je pense à l'absurde, ou la récurrence, ou les deux ...
Si on a un 4, qu'est-ce qu'on a eu avant pour en arriver là ?
exactement, si on a un 4, qu'est-ce qu'on a eu avant pour en arriver là???
on avait bien triper avec un de mes meilleurs potes, aussi prof de math, sur la démo durant un apéro fortement appuyé...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 08 Oct 2009, 12:39
par Timothé Lefebvre » 08 Oct 2009, 12:39
Lol, ça peut être intéressant mais là j'ai un cours à 3h (dans 3 minutes pile lol), et donc je n'ai pas trop le temps !
-
adrd
- Membre Naturel
- Messages: 75
- Enregistré le: 04 Avr 2009, 09:00
-
 par adrd » 09 Oct 2009, 15:03
par adrd » 09 Oct 2009, 15:03
Bonjour,
On peut le démontrer par l'absurde.
Supposons qu'il y ai un 4.
Dans le nombre précèdent, il y aurait quatre fois le même chiffre ...AAAA....
C'est à dire que dans le nombre encore avant il y aurait :
- A fois le chiffre A suivi de A fois le chiffre A
et c'est égal à 2A fois le chiffre A donc c'est impossible
- ou B fois le chiffre A suivi de A fois le chiffre A suivi de A fois le chiffre C
et c'est égal à A+B fois le chiffre A suivi de A fois le chiffre C donc c'est impossible.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 09 Oct 2009, 16:58
par ffpower » 09 Oct 2009, 16:58
Exact.Pour completer la demo,faut juste dire qu on prend le 1er nb ou ya un 4(ou plus)...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 10 Oct 2009, 12:12
par Ericovitchi » 10 Oct 2009, 12:12
Ha oui fascinant cette suite de Conway. Sur Wikipedia on trouve que :
* Le nombre de chiffres du ne terme de la suite est proportionnel à

n, où
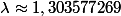
est un nombre algébrique de degré 71 nommé constante de Conway. Plus précisément, si on note Ln le nombre de chiffre du ne terme de la suite, alors :
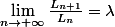
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités