Connexité simple

[Borriello]

Bjr,

Pourriez-vous m'aider cette question : est-ce que l'espace projectif complexe est simplement connexe ? Et comment le démontrer ?

Merci d'avance

[Finrod]

est un cercle et une sphère.

A première vue, ils ont pas l'air connexe respectivement dans le plan et l'espace.

(je ne m'étais jamais posé la question)

[Nightmare]

Salut !

Eh bien, on a un homéomorphisme entre l'espace projectif complexe et la sphère donc...

[Borriello]

Merci pour votre aide.

Oui, le cas est clair, mais le cas où , comment vous le traitez ?

[mathelot]

bonjour,

j'espère ne pas écrire trop de bêtises :hum:


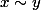ssi

On peut considérer x et y sur la sphère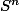 et le modulo selon des coefficients multiplicatifs , nombres complexes de module 1,donc de la forme

on a la projection canonique

qui envoie un point de l'espace affine privé de l'origine sur sa direction
de "droite".

Cette projection est continue, surjective et sans doute que chaque
image réciproque d'un point de l'espace projectif est un cercle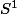
puisque , sur la sphère, on travaille modulo un coeff multiplicatif
de module 1.

question
est-ce qe cette projection canonique est un revêtement. Il semble
que oui. ie,
pour des ouverts V suffisemment petits.

le problème serait de trivialiser ce revêtement pour remonter un lacet de l'espace projectif , peut être pas en un lacet, mais tout au moins en un chemin. notons ce chemin

on a donc


maintenant si l'on parcourt le chemin L sur la sphère de a' vers b'
puis en sens inverse selon défini par , la concaténation des deux chemins
est un lacet, homotope à un point , la sphère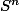 étant simplement connexe.

Dès lors, on peut composer cette homotopie avec la projection canonique p.

Le problème semble être de trivialiser un revêtement.

sinon, il y a quelques outils de topologie à disposition:
tous les ensembles fermés sont compacts car les espaces ambiants (sphère et espace projectifs le sont)
Les surfaces de Riemann ont toutes un revêtement universel. Est-ce que cela permet de "factoriser" des applications (par exemple , un lacet) selon un diagramme commutatif ?

[Borriello]

Merci pour votre aide,

Je rajoute la raison pour laquelle j'ai posé la question au-dessus : si on peut démontrer la connexité simple de , on démontrera que toute application holomorphe de dans un tore est constante

[mathelot]

Merci pour votre aide,

Je rajoute la raison pour laquelle j'ai posé la question au-dessus : si on peut démontrer la connexité simple de , on démontrera que toute application holomorphe de dans un tore est constante

est-ce que l'on peut appliquer les formules de Cauchy dans des cartes ?
comment ça se passe ?

[Borriello]

Quelles sont les formules de Cauchy ?

Il y a un théorème qui permet d'affirmer ça . Tu peut lire le théorème 4.17 dans "Lectures on Riemann Surfaces" d'Otto Forster :

Suppons que X et Y soient espaces séparés et un revêtement . Suppons que Z soit simplement connexe, connexe par arcs et localement connexe par arcs, et une application continue. Alors pour chaque point de Z et de Y tels que , il y a précisément un relèvement tel que

Mon français est peut-être difficile à comprendre, tu devrais donc lire dans le livre