Formule cosinus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 11:07
par Edward » 04 Oct 2009, 11:07
Bonjour,
J'ai un petit : je n'arrive pas à calculer : produit de k = 1 à n des cosinus (1/k). J'ai essayé 2,3 trucs (utiliser la formule sin(2x) = sinx cosx par exemple) mais je n'arrive à rien... je dois louper quelque chose.
Quelqu'un pourrait-il m'aider ?
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 11:10
par skilveg » 04 Oct 2009, 11:10
Salut,
Il vient d'où cet exo? Tu es sûr que ce n'est pas plutôt quelque chose du genre

?
(Par ailleurs ta formule est incorrecte en général, c'est
=2\sin x\cos x)
.)
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 11:14
par Edward » 04 Oct 2009, 11:14
J'oublie toujours le 2 dans la formule...
Sinon oui je suis sur que c'est cos(1/k).
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 11:29
par skilveg » 04 Oct 2009, 11:29
Il ne me semble pas qu'il y ait de forme simple... Tu l'as trouvé où cet énoncé?
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 11:40
par Edward » 04 Oct 2009, 11:40
Un exercice sur les séries : je doit trouver la nature de la série de terme général
ln ( cos (1 / n ) ).
Si on écrit l'expression de la some partielle on peut utiliser la formule
ln(a) + ln(b) = ln(a*b), et on se retrouve avec ln du produit que je cherche.
En fait il suffirait de montrer que le produit en question tend vers une limite non nulle.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 11:44
par skilveg » 04 Oct 2009, 11:44
Je pense que ce n'est pas la bonne méthode (tu ne trouveras pas de forme simple pour ton produit); le mieux est de faire un développement asymptotique du terme général de ta série quand

tend vers l'infini.
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 11:47
par Edward » 04 Oct 2009, 11:47
Je ne vois pas comment ça m'aide à conclure. Comment je repasse à ma série une fois le DA établi ?
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 11:58
par skilveg » 04 Oct 2009, 11:58
Dans ton cours tu as des théorèmes de sommation des relations de comparaison qui permettent de savoir si une série converge ou pas en regardant le DA du terme général.
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 12:16
par Edward » 04 Oct 2009, 12:16
Comme DA je trouve
)=-\frac{1}{2n^2}+o\left(\frac{1}{n^2}\right))
.
Si j'ai bien compris je dois trouver un grand tau d'une suite dont la somme partielle converge, c'est ça ?
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 12:30
par skilveg » 04 Oct 2009, 12:30
Si c'est le bon développement asymptotique, tu as terminé: si
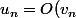)
où

est sommable, alors

est sommable (écrire la définition du grand O). Et comme on sait ce qui se passe pour
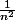
...
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 12:33
par Edward » 04 Oct 2009, 12:33
Justement c'est sur le 1 / n^2 que je bloque...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Oct 2009, 13:30
par Ericovitchi » 04 Oct 2009, 13:30
Pour info
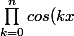 = \frac{sin(\frac{n+1}{2}x)}{sin (\frac{x}{2})} cos(n \frac{x}{2}))
Et
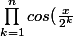 = \frac{1}{2^n}\times\frac{sin(x)}{sin(\frac{x}{2^n})})
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 13:35
par skilveg » 04 Oct 2009, 13:35
Edward, qu'est-ce que tu peux dire de la série

?
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 13:45
par Edward » 04 Oct 2009, 13:45
Je suppose que je devrais répondre convergente mais je vois pas trop pour quoi ...
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Oct 2009, 13:53
par skilveg » 04 Oct 2009, 13:53
Un argument-massue: c'est une série de Riemann. Un argument plus léger: on a
}=\frac{1}{n-1}-\frac{1}{n})
, qui donne une série télescopique.
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 04 Oct 2009, 14:02
par Edward » 04 Oct 2009, 14:02
Pas bête du tout ! Merci pour ta patience Skilveg :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
