Parties finies, nombres complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 03 Oct 2009, 12:54
par gilles3 » 03 Oct 2009, 12:54
Bonjour, j'ai un exo de math un peu difficile sur lequel je bloque
le voilà: soit

un nombre complexe.
Existe-il des parties finies

de C qui vérifient les conditions (i) et (ii).
(i)
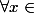
C,
^2 \in)
C
(ii)
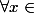
C,
^2 \in)
C
Je vois du tout comment commencer
-
SimonB
 par SimonB » 03 Oct 2009, 13:16
par SimonB » 03 Oct 2009, 13:16
L'énoncé gagnerait à prendre du sens en étant corrigé de manière exacte : le quantificateur parle de x, la phrase logique qui suit parle de z... D'autre part, pour tout complexe z, (z+1)² est dans C...
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 03 Oct 2009, 13:35
par gilles3 » 03 Oct 2009, 13:35
Je suis vraiment désolé.
le voilà (correctement): soit z un nombre complexe.
Existe-il des parties finies A de C qui vérifient les conditions (i) et (ii).
(i)

,
^2 \in A)
(ii)

,
^2 \in A)
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 03 Oct 2009, 14:26
par wserdx » 03 Oct 2009, 14:26
Recherche les expressions des termes des suites
définies par la relation de récurrence
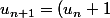^2)
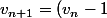^2)
Essaie de trouver

et
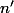
pour lesquelles les équations
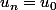

ont des racines communes.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Oct 2009, 14:37
par yos » 03 Oct 2009, 14:37
>2|z|)
donc soit

soit

est strictement supérieur à |z|. Donc ton ensemble ne saurait être fini.
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 03 Oct 2009, 16:19
par gilles3 » 03 Oct 2009, 16:19
oui je suis tout à fait d'accord avec votre réponse sur les modules de z+1, z-1, et z mais je ne vois toujours pas comment aboutir au résultat.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 03 Oct 2009, 16:34
par wserdx » 03 Oct 2009, 16:34
En effet, j'ai proposé une méthode pour essayer de construire A.
ça aurait pu marcher avec

et

par exemple.
Mais l'argument donné qui montre que A ne peut être fini est imparable.
Si A vérifie (i) et (ii), on peut extraire une suite de termes dont les modules
sont strictement croissants, donc infinie.
-
gilles3
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Avr 2009, 18:41
-
 par gilles3 » 03 Oct 2009, 18:01
par gilles3 » 03 Oct 2009, 18:01
ah oui j'ai compris là
merci beaucoup pour vos explications.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités