Opérateur compact associé au problème de Dirichlet

par **melreg** » 25 Sep 2009, 08:32

Bonjour,

J'aimerais savoir comment montrer que l'opérateur

,

où

satisfait:

pour

un ouvert borné de

et où

désigne le laplacien.
Dans mon livre, la justification est: "c'est une conséquence immédiate du théorème de Rellich".
Du coup, je me dis que je dois passer à côté de l'essentiel, mais je ne vois vraiment pas.

Merci d'avance à vous de vous pencher sur mon problème.

par **ffpower** » 25 Sep 2009, 09:01

euh,c est quoi la question?^^

par **Finrod** » 25 Sep 2009, 09:03

Tu as oublié de le dire mais tu veux montrer qu'il est compact.

cela revient à dire que tu veux que l'image d'une partie bornée de L^{2} soit compacte.

Si E est une telle partie et M est sa borne pour la norme ||-||_{2}, T(E) est composé de fonction L^{2}, u dont le laplacien est borné en norme L^{2}.

Pour montrerque c'est compact, tu montres que toute suite admet une sous-suite convergent.

Soit donc (u_{n}) une suite dans T(E)

Je te conseille de regarder le theorme de Rellich pour obtenir une sous suite convergente dans L^{2} puis de vérifier que l'ona une sous suite de cette sous suite convergente dans H^{1}_{0} en utilisant le fait que la dérivée 2nd est bornée en norme L^{2}

par **melreg** » 25 Sep 2009, 09:41

Merci Finrod pour ta réponse... et aussi pour avoir deviné la question!!!
Je vais regarder ça (et comme tu me le conseilles, de me plonger dans la preuve du théorème de Rellich) de plus près et je redonne des nouvelles ensuite.

par **Finrod** » 25 Sep 2009, 09:54

Tu peux regarder la preuve de Rellich (c'est très bien) , mais je ne te l'ai pas demandé ^^! . Je dis juste que ce thm affirme que tu peux trouver une sous-suite convergente dans L^{2}.

par **melreg** » 25 Sep 2009, 12:01

En fait, on veut montrer que l'image par

de toute partie bornée est relativement compacte (et non pas compacte). Une autre manière de voir que

est compact est de montrer que l'image par

de toute suite faiblement convergente est convergente.

Voilà le début de mon raisonnement: Soit

une suite dans

telle que

converge faiblement vers

dans

. Considérons la suite

dans

. Par définition des

,

.
Mais après, je ne vois pas comment montrer que

converge (en fait converge vers

).

Une idée? Je vous en serais très reconnaissant!

par **Finrod** » 25 Sep 2009, 12:42

Alors, au niveau du formalisme, faiblement convergent, fais référence à une convergence en norme L^{2}, c'est bien ça ?

La convergence à l'arrivée se détermine par contre par la norme de H^{1}, donné par le produit scalaire présent ici
http://fr.wikipedia.org/wiki/Espace_de_Sobolev#H1.28.CE.A9.29_et_H10.28.CE.A9.29
en bas de la page.

enfin, normalement, comme je suis un peu rouillé sur ça...

Donc : T(f_{n}) est une suite dont les éléments sont dans L^{2} et ont des dérivées partielles dans L^{2} (j'avais fait un lapsus dans le message précédant, je parlais du laplacien dans L^{2}, ce n'est pas la définition).

Il faut vérifier d'abord que la suite est bornée, pour la norme de H^{1}.

Il manque des infos pour continuer. J'ai jeter un coup d'oeil, peut être l'inégalité de poincarré, qui est censé être une conséquence de Rellich peut aider. Cette inégalité donne entre autres

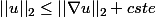
en particulier

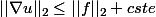
Bon ça ça prouve que c'est borné en norme H^{1}. Maintenant la suite :

En appliquant la véritable inégalité de poicarré, il est clair en fait que l'on a convergence H^{1}... A moins que je vois mal.
L'inégalité est là : http://en.wikipedia.org/wiki/Rellich-Kondrachov_theorem

par **melreg** » 25 Sep 2009, 14:39

Finrod a écrit: en particulier

Il me semble que tu n'oses pas appliquer cette inégalité à

car

or l'égalité de poincaré est justement valable pour des fonctions dans

.

Mais si on avait ça, mon problème serait reglé...

En fait, si on montre que

est borné, c'est bon. En effet, l'image d'une partie borné

de

par

serait alors bornée dans

et comme l'injection de

dans

est compacte (théorème de Rellich),

serait alors précompacte (ce que l'on veut). Mais est-ce que

est bornée??

par **Finrod** » 25 Sep 2009, 14:45

C'est bizarre, dans wikipédia, ils donnent cette égalité pour tout fonction de H^{1} (ou W^{1,2})...

Mais aprés vérification,tu as raison : La page de wikipédia en anglais est fausse, celle en français est juste.

on en tirera au moins une moindre satisfaction chauviniste.

Si je vois autre chose, je le dirai.

J'espère que tu trouveras un géomètre différentiel potable, le pauvre géomètre algébriste que je suis ne peut plus rien pour toi ^^
Bon courage.

par **melreg** » 25 Sep 2009, 14:57

Merci Finrod. Je galère pour montrer ça, c'est terrible. Surtout que dans mon bouquin, c'est écrit en gros: "trivial"... :mur:

par **Finrod** » 25 Sep 2009, 15:17

Non mais ça ça arrive tout le temps ^^

J'ai galéré une journée entière la semaine dernière sur un produit semi direct soit disant évident d'anneaux qui impliquait un produit semi-direct de faisceaux en groupes.

Bon ben il manquait un exposant "n" dans le papier "évident" alors évidemment...

etc...
ps: c'est quoi ton bouquin ?

par **melreg** » 28 Sep 2009, 06:19

C'est un bouquin assez connu je crois. Et ici, je ne pense pas qu'il manque quelque chose. En fait, l'auteur passe en vitesse sur ce genre de résultat, pour ce concentrer sur l'aspect géomètrique des choses...

Le livre c'est: "Extremum problems for eigenvalues of elliptic operators" de Henrot.

par **Finrod** » 28 Sep 2009, 14:12

J'ai jeté un coup d'oeil au bouquin sur google books.

Je pense que je vois.
C'est peut être une question formelle (c'est les pires)

Rellich implique que l'on a en fait la relative compacité de l'image dans L^{2}.

1.10 implique que la norme H^{1} de u est majoré par le produit scalaire de f et u dans L^{2}, lui même, si mes vieux souvenirs ne me trahissent pas, majoré par le produit des normes (peut être fois une cste).

Cela ne suffit il pas ?

par **ShakkaChan** » 28 Sep 2009, 22:50

normalement c'est en effet imédiat par Reillich tu dis juste que puisque H1 s'injecte compactement dans L2 alors l'operateur est compact dans L2. a priori pas besoin de plus de justification

par **melreg** » 29 Sep 2009, 07:03

Finrod a écrit:J'ai jeté un coup d'oeil au bouquin sur google books.

Je pense que je vois.
C'est peut être une question formelle (c'est les pires)

Rellich implique que l'on a en fait la relative compacité de l'image dans L^{2}.

1.10 implique que la norme H^{1} de u est majoré par le produit scalaire de f et u dans L^{2}, lui même, si mes vieux souvenirs ne me trahissent pas, majoré par le produit des normes (peut être fois une cste).

Cela ne suffit il pas ?

Je pense que ça devrait aller. Peut-être que l'inégalité de Poincaré sera utile.
Merci de ton aide!

par **melreg** » 29 Sep 2009, 07:07

ShakkaChan a écrit:normalement c'est en effet imédiat par Reillich tu dis juste que puisque H1 s'injecte compactement dans L2 alors l'operateur est compact dans L2. a priori pas besoin de plus de justification

Ben je ne comprends pas pourquoi ça suffit (et finrod non plus visiblement). En fait, pour montrer que l'opérateur est compact, on prend une partie bornée de

; si l'image par l'opérateur de cette partie est bornée dans

, alors, par compacité de l'injection, elle sera bornée dans

.
Le problème que j'avais était de voir pourquoi l'image de la partie bornée était elle-même bornée (les espaces de départ et d'arrivée n'étant pas les mêmes).

Mais si, en effet, c'est "trivial", je veux bien savoir pourquoi?

Merci à toi de te pencher sur ce problème.

par **kazeriahm** » 29 Sep 2009, 09:30

Wahou ! Tu connais Henrot ? C'est mon prof ! Tout petit moment de gloire...

par **melreg** » 29 Sep 2009, 10:59

kazeriahm a écrit:Wahou ! Tu connais Henrot ? C'est mon prof ! Tout petit moment de gloire...

Moi pas, j'utilise juste son livre...

par **ShakkaChan** » 29 Sep 2009, 18:45

je vais utiliser un autre caractérisation d'un operateur compact mais avec un peu d'effort ca doit marcher avec la définition avec l'image de boule unité.

prend la caractérisation d'un operateur compact page 2 de ce document
ici l'injection de H1 dans L2 compact veux dire que l'identité de H1 vers L2 est compact ( je nomme cette identité ID) donc par la caractérisation si

Un cv faible vers 0
ID(Un) cv fort vers 0

on compose par ton operateur T ca va donner ton operateur mais de L2 dans L2 au lieu de L2 dans H1

on a donc T(ID(Un)) cv fort vers T(0) T etant linéaire T(0)=0 donc on a bien

T composé avec ID de Un qui converge vers 0
par conséquent T composé avec ID est compact. par conséquent T de L2 dans L2 est compact
Je pense que cette démo est bonne (pas sur a 100%)
qu'en pense tu ?

Ps j'ai pas dis que c'etait trivial mais dans un devoir t'es pas obliger de justifer en detail

par **ShakkaChan** » 29 Sep 2009, 18:51

si tu regarde le document que j'ai mis en lien tout ca est traité ainsi que ces applications. par exemple page 14 15 pour la decomposition spectrale du laplacien

Opérateur compact associé au problème de Dirichlet

opérateur compact associé au problème de Dirichlet

Qui est en ligne